补码的前世今生
计算机如何来保存负数呢?其实只要达到这样的目的:正数负数都有一个唯一标识即可,但是,正如人类用+1和-1来表示可以提高效率一样,也得有一个比较适当的适合我们的计算机识别的一个方式。下面来详细讲解。
问题的由来
下面为了表示方便,先假设存储一个整型数字用4个bit。
举例来说,+2在计算机中表示为二进制的0010,那么-2怎么表示呢?
很容易想到,可以将一个二进制位(bit)专门规定为符号位,它等于0时就表示正数,等于1时就表示负数。比如,在8位机中,规定每个字节的最高位为符号位。那么,+2就是0010,而-8则是1010。
更多的例子如下:
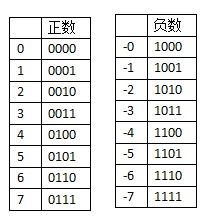
这就是直接用原码的方式来存储,虽然说这种方式理论上是可行的,毕竟每个数我都唯一标识了。
但是这种方式存在问题,我们希望+1和-1相加为0,但是通过这个方式算出来的是:0001+1001=1010 (-2)。也就是说,按照正常一步头的方式得不到我们想要的结果。
为了解决了“正负相加等于0”的问题,人们发明了反码。
反码
“反码”表示方式是用来处理负数的,符号位置不变,其余位置相反。
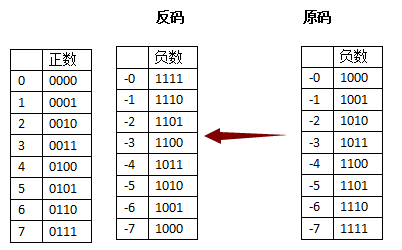
此时,我们再来算一下+1和-1相加,变成了0001+1110=1111,刚好反码表示方式中,1111象征-0。
此时,好像是解决了这个问题,但是我们发现,0这个时候有了两种表达:0000和1111。
即在用反码表示的情况下,0竟然可以用两个值来表示,这显然不好吧。毕竟+0和-0就是同一个玩意啊。
这个时候补码闪亮登场。
补码
很简单,在刚才反码的基础上加1。
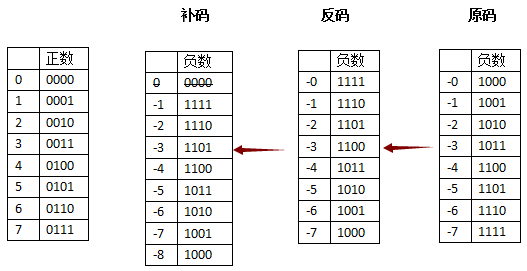
此时,我们这里假定整形只有4位。那么-0表示为1111+1=10000,显然溢出了,就需要丢弃最高位,变成0000.
此时,神奇地发现,达到了统一,+0和-0都是用0000来表示了。
此时,也满足正负数相加为0的条件。比如+2为0010,-2为1110.此时两者相加为:0010+1110=(0)0000,丢掉最高位就是0000
那么对于普通情况,比如7+(-4)呢?即0111+1100=0011,就是3。OK,大功告成。
补码怎么求
上面已经说的很详细啦,比如-4,就是在4(0100)的基础上取反(1011)再加一(1100).
上面也解释了为什么要用补码。即保证了对称的正负数相加为0并且0只有一种表示方式。
还有一个重要的点就是,我们注意到,7-4其实我们都是转换成7+(-4),也就是说,在计算机中,减法都是用加法的逻辑实现的。
即:一套加法的电路实现加减法。此外,乘法和除法其实都是加法这套电路实现的。
补码的本质
这里假设存储一个整型用8个bit。
要将正数转成对应的负数,其实只要用0减去这个数就可以了。比如,-8其实就是0-8。
则8的二进制是00001000,-8就可以用下面的式子求出:
1 | 00000000 |
因为00000000(被减数)小于0000100(减数),所以不够减。请回忆一下小学算术,如果被减数的某一位小于减数,我们怎么办?很简单,问上一位借1就可以了。
所以,0000000也问上一位借了1,也就是说,被减数其实是100000000,算式也就改写成:
1 | 100000000 |
进一步观察,可以发现100000000 = 11111111 + 1,所以上面的式子可以拆成两个:
1 | 11111111 |
通过这一步,我们就从数学上知道了为什么补码是取反加一了。
你看,求任何一个负数,都是0-正数,那么就用借位的思想来,则变成100000000。
100000000则可以分解为11111111+00000001。
此时求负数的过程就就变成11111111-X+1
- 而先用11111111来减这个正数,这个结果就是对正数取反。
- 此时再加上另外一个1.
这与我们求补码的过程是一样的,这也解释了为什么要这样求补码。
证明(可不看)
将上面的特例抽象一下,用统一表达式来证明一下。
我们要证明的是,X-Y或X+(-Y)可以用X加上Y的补码完成。
Y的补码等于(11111111-Y)+1。所以,X加上Y补码,就等于:
1 | X + (11111111-Y) + 1 |
我们假定这个算式的结果等于Z,即
1 | Z = X + (11111111-Y) + 1 |
接下来,分成两种情况讨论。
- 第一种情况,如果X小于Y,那么Z是一个负数。
由Y的补码等于(11111111-Y)+1,标记为F=(11111111-Y)+1,那么如何根据F逆向求Y呢?
1 | Y=1111111-(F-1) |
OK,因为此时Z是一个负数,那么Z进行补码的逆运算就可以求出它的绝对值,即正数。再加一个符号,两者相等。
1 | Z = -[11111111-(Z-1)] = -[11111111-(X + (11111111-Y) + 1-1)] = X - Y |
- 第二种情况,如果X大于Y
这意味着Z肯定大于11111111,但是我们规定了这是8位机,最高的第9位是溢出位,必须被舍去,这相当于减去100000000。所以,
1 | Z = Z - 100000000 = X + (11111111-Y) + 1 - 100000000 = X - Y |
这就证明了,在正常的加法规则下,可以利用2的补码得到正数与负数相加的正确结果。换言之,计算机只要部署加法电路和补码电路,就可以完成所有整数的加法。
本文整理自: