无论在什么业务中，钱是非常重要的东西，对账的时候一定要对的上，不能这边少一分那边多一分。对于数值的计算，尤其是小数，double和double都是禁止使用的。

阿里强制要求存放小数时使用 decimal，禁止使用 float 和 double。

说明：float 和 double 在存储的时候，存在精度损失的问题，很可能在值的比较时，得到不正确的结果。如果存储的数据范围超过 decimal 的范围，建议将数据拆成整数和小数分开存储。

处理方式可以为：mysql 可以用 decimal ，如果你是用 java， 在商业计算中我们要用 java.math.BigDecimal，注意：如果需要精确计算，非要用String来够造BigDecimal不可！

那么到底是什么情况？

一个例子说明

废话不多说，上图：

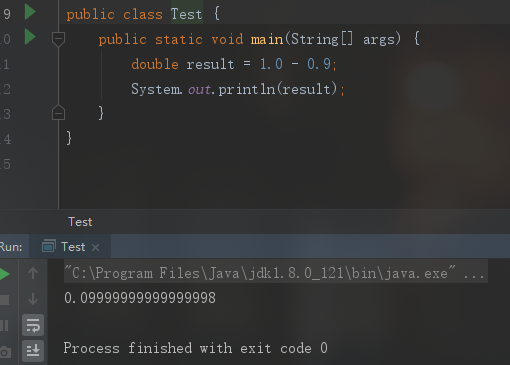
image

问题原因

无论是我们本文提到的double，还是float，都是浮点数。

在计算机科学中，浮点（英语：floating point，缩写为FP）是一种对于实数的近似值数值表现法，由一个有效数字（即尾数）加上幂数来表示，通常是乘以某个基数的整数次指数得到。以这种表示法表示的数值，称为浮点数（floating-point number）。

其实我觉得很好理解，我们之前说过，计算机计算加减乘除啊，都是用的加法器，实质都是二进制的加法处理。那么这里就有一个二进制表示的问题。试想，4，2，8之流都是2的幂次方，可以完美用二进制表示，计算当然不会出现问题。对于0，1，3，5之类也都可以用二进制来表示出来，所以，正数肯定是没问题的。

但是对于小数呢？1、0.5、0.25那都是可以转换成二进制的小数，如十进制的0.1，就无法用二进制准确的表示出来。因此只能使用近似值的方式表达。

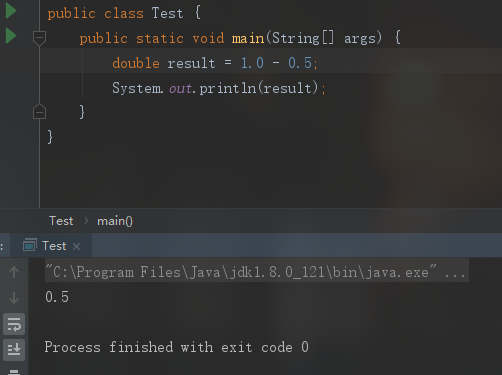
image

如果我们尝试着把10进制的0.1转化成二进制，会怎么转呢？

在十进制中，0.1如何计算出来的呢？

0.1 = 1 ÷ 10

那么二进制中也是同理：

1 ÷ 1010

我们回到小学的课堂，来列竖式吧：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
       0.000110011...
      ------------------
1010 ) 1 0000
         1010
       ------
          1100
          1010
          ----
            10000
             1010
            -----
              1100
              1010
              ----
                10

很显然，除不尽，除出了一个无限循环小数：二进制的 0.0001100110011…

那么，如何在计算机中表示这个无限不循环的小数呢？只能考虑按照不同的精度保理不同的位数。

我们知道float是单精度的，double是双精度的。不同的精度，其实就是保留的有效数字位数不同，保留的位数越多，精度越高。

所以，浮点数在Java中是无法精确表示的，因为大部分浮点数转换成二进制是一个无限不循环的小数，只能通过保留精度的方式进行近似表示。

问题的解决

String 构造方法是完全可预知的：写入 newBigDecimal("0.1") 将创建一个 BigDecimal，它正好等于预期的 0.1。因此，比较而言，通常建议优先使用String构造方法。

使用BigDecimal(String val)！

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
//加法
public static BigDecimal add(double v1, double v2){
    BigDecimal b1 = new BigDecimal(Double.toString(v1));
    BigDecimal b2 = new BigDecimal(Double.toString(v2));
    return b1.add(b2);
}

//减法
public static BigDecimal sub(double v1,double v2){
    BigDecimal b1 = new BigDecimal(Double.toString(v1));
    BigDecimal b2 = new BigDecimal(Double.toString(v2));
    return b1.subtract(b2);
}

//乘法
public static BigDecimal mul(double v1,double v2){
    BigDecimal b1 = new BigDecimal(Double.toString(v1));
    BigDecimal b2 = new BigDecimal(Double.toString(v2));
    return b1.multiply(b2);
}

//除法
public static BigDecimal div(double v1,double v2){
    BigDecimal b1 = new BigDecimal(Double.toString(v1));
    BigDecimal b2 = new BigDecimal(Double.toString(v2));
    return b1.divide(b2,2,BigDecimal.ROUND_HALF_UP);//四舍五入,保留2位小数,应对除不尽的情况
}

那么，上面的精度丢失问题就迎刃而解了。但是除不尽怎么办？比如10.0除以这里的3.0，保留小数点后三位有效数字：

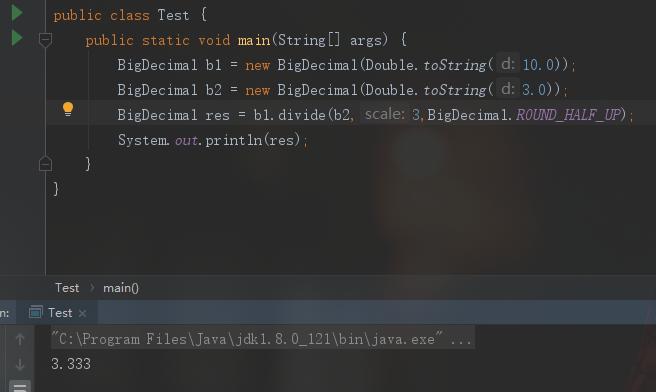
image

那么，每个用户得到的都是3.333元，三个用户加起来是得不到10块钱的。

对于除法，始终会产生除不尽的情况怎么办？有个词叫轧差

什么意思呢？举个简单例子。假如现在需要把10元分成3分，如果是10除以3这么除，会发现为3.33333无穷尽的3。这些数字完全无法在程序或数据库中进行精确的存储。

简单理解就是，当除不尽或需去除小数点的时候，前面的n-1笔（这里n=3）做四舍五入。最后一笔做兜底（总金额减去前面n-1笔之和）。这样保证总金额的不会丢失。

比如10块钱，三个用户分，前面两个用户只能各分到3。333块钱，最后一个用户分到3.334块钱。保证总额不变。

至于原理，有一点点数学化，以后再作探讨吧。