基础算法1-递归入门

算法入门系列以递归开头，我们知道，递归的编码往往是比较简单的，但是递归的思想往往又是难以理解。在写完这篇笔记之后仍然无法得递归之要领，不过对于如何写递归是有了一定得章法，一句话就是用数据归纳法，先尝试n得情况，再去考虑0或者1得情况，并且保证范围在逐渐缩小并且一定可以结束，下面我们来详细说一说递归。

一、什么是递归

我们可以把”递归“比喻成”查字典“，当你查一个词，发现这个词的解释中某个词仍然不懂，于是你开始查这第二个词。

可惜，第二个词里仍然有不懂的词，于是查第三个词，这样查下去，直到有一个词的解释是你完全能看懂的，那么递归走到了尽头，然后你开始后退，逐个明白之前查过的每一个词，最终，你明白了最开始那个词的意思。（摘自知乎的一个回答）

从程序本身来看，就是一个函数直接或间接调用自身的一种方法，它通常把一个大型复杂的问题层层转化为一个与原问题相似的规模较小的问题来求解。

我们这里以计算阶乘为切入点：

int Factorial(int n){    

      if (n == 0)  return 1;  

      return n * Factorial(n - 1);

}

我们以上述代码为例，取 n=3，则过程如下：

第 1~4 步，都是入栈过程，Factorial(3)调用了Factorial(2)，Factorial(2)又接着调用Factorial(1)，直到Factorial(0)；

第 5 步，因 0 是递归结束条件，故不再入栈，此时栈高度为 4，即为我们平时所说的递归深度；

第 6~9 步，Factorial(0)做完，出栈，而Factorial(0)做完意味着Factorial(1)也做完，同样进行出栈，重复下去，直到所有的都出栈完毕，递归结束。

可以看出来，递归的本质就是由一个系统栈不停地保存每一层调用的方法及其参数，直到遇到终止条件为止，一层一层地结束返回，但是当层数过深的时候就有可能出现stack overflow这样的栈溢出错误。

也可以看出来，每一个递归程序都可以把它改写为非递归版本。但是并不是每个递归程序都是那么容易被改写为非递归的。某些递归程序比较复杂，其入栈和出栈非常繁琐，给编码带来了很大难度，而且易读性极差，所以条件允许的情况下，推荐使用递归。

二、如何思考递归

在初学递归的时候, 看到一个递归实现, 我们总是难免陷入不停的验证之中，比如上面提及的阶乘，求解Factorial(n)时，我们总会情不自禁的发问，Factorial(n-1)可以求出正确的答案么？接着我们就会再用Factorial(n-2)去验证，，，不停地往下验证直到Factorial(0)。

对递归这样的不适应，和我们平时习惯的思维方式有关。我们习惯的思维是：已知Factorial(0)，乘上 1 就等于Factorial(1)，再乘以 2 就等于Factorial(2)，，，直到乘到 n。

因此，递归和我们的思维方式正好相反。这就会给我们编程造成相当大的思维干扰。

其实，递归的数学思想是数学归纳法：

如果下面这两点是成立的，我们就知道这个递归对于所有的 n 都是正确的。
1）当 n=0,1 时，结果正确；
2）假设递归对于 n 是正确的，同时对于 n+1 也正确。

在递归中，我们通常把第 1 点称为终止条件，因为这样更容易理解，其作用就是终止递归，防止递归无限地运行下去。

对于第二点就是假定如果n-1的情况是正确的，那么n的情况就是正确的，然后再假定n-2的情况是正确的，那么n-1的情况也是正确的，那么就会一直推导到特殊情况比如0的时候，这个时候是正确的，那么前面所有的都是正确的。

从而达到了上面说的，将一个复杂的问题一层一层地转化为相似的小规模的问题，这样，解决了小规模问题之后一层一层地就可以返回来求出复杂的问题。

根据数学归纳法，其实我们还可以归纳出编写递归程序的一些准则：

严格定义递归函数作用，包括参数、返回值、side-effect
先一般再特殊
每次调用必须缩小问题规模
每次问题规模缩小程度必须为1

这里简单地再解释一下，第一条中注意的是side-effect，这些是一些存储状态的变量，比如一些全局的变量来控制递归里面的一些逻辑等等。

考虑问题的时候可以从特殊的问题来考虑，但是在编写递归程序的时候，最好是先考虑一般的场景，最后再来看特殊的场景从而终止递归。并且每次缩小程度为1，不能为2或者3等。

好了，其实递归真正说起来好像也就那回事，但是真正用好确实是需要大量的训练，即递归的思维训练。

三、递归的方式创建单向链表

首先定义一下链表类：

public class Node {
    private final int val;
    private Node next;

    public Node(int val){
        this.val = val;
        next = null;
    }

    public int getVal() {
        return val;
    }

    public Node getNext() {
        return next;
    }

    public void setNext(Node next) {
        this.next = next;
    }

    //打印链表
    public static void print(Node head){
        while (head != null){
            System.out.print(head.val+"->");
            head = head.next;
        }
        System.out.print("null");
        System.out.println("");
        System.out.println("======================================");
    }
}

假设有一个数组：1，2，3，4，5，目标是将它们转换为链表。

正常的思维是：创建节点node1，node2，然后node1的next指向node2，依次类推直到最后。但是用递归的时候就不要这么想了，我们的思维方式变为：

假设2，3，4，5已经组装好了，那么我只需要再将1插到这个组装好的链表的最前面即可：

那么，首先我们确定函数参数，返回值等：

1
2
3

public Node createLinkedList(List<Integer> values){
    
}

那么，首先，我取出1作为firstNode，然后我这个1指向的是后面已经排好的(2->3->4->5)这个链表，此时不就成功了嘛！

public Node createLinkedList(List<Integer> values){
    //获取数组第一个元素
    Node firstNode = new Node(values.get(0));
    //获取后面排好的链表的头节点
    Node fisrtSubNode = createLinkedList(values.subList(1,values.size()));
    //第一个元素指向后面排好的链表的头节点即可
    firstNode.setNext(fisrtSubNode);
    //返回整个链表的头节点
    return firstNode;
}

此时，我们只要知道：createLinkedList(values.subList(1,values.size()));这个就可以帮助我们拼接成我们需要的(2->3->4->5)这个链表，下面我只需要将1指向这个链表就可以成功了。我们仔细来看这个函数，就是调用自身，即递归，里面参数是：除了第一个元素外剩余的元素，并且每一层就剔除掉第一个元素，那么此时还需要一个终止条件，就是这个数组已经没有元素了就停止。所以完整的程序是：

public Node createLinkedList(List<Integer> values){
    //5.递归停止的条件就是没有元素了
    if (values.size() == 0){
        return null;
    }
    //1.获取数组第一个元素
    Node firstNode = new Node(values.get(0));
    //2.获取后面排好的链表的头节点，用subList来截取，逐渐地截短使得问题的规模变小
    Node fisrtSubNode = createLinkedList(values.subList(1,values.size()));
    //3.第一个元素指向后面排好的链表的头节点即可
    firstNode.setNext(fisrtSubNode);
    //4.返回整个链表的头节点
    return firstNode;
}

我们可以想象，一层一层地剔除第一个元素，过程是(2->3->4->5)，(3->4->5)，(4->5)，（5)，()，此时为空了停止，就会返回到上一层执行的地方，即Node fisrtSubNode = null这一句，此时，上一层的firstNode就是5，那么继续执行就是5.setNext(null)，return 5，这一层又结束了返回到上一层，上一层此时firstNode=4，那么fisrtSubNode = 5，然后继续执行就是4.setNext(5)，最后return 4，此时链表已经是4->5->null了，再重复以上的过程直到2->3->4->5->null，此时回到最上层，即一开始的地方，即假定1后面就是拼接好的链表，此时确实也是拼接好的。所以这里用的就是数学归纳法的思想。

四、递归的方式反转单向链表

链表的反转效果为：

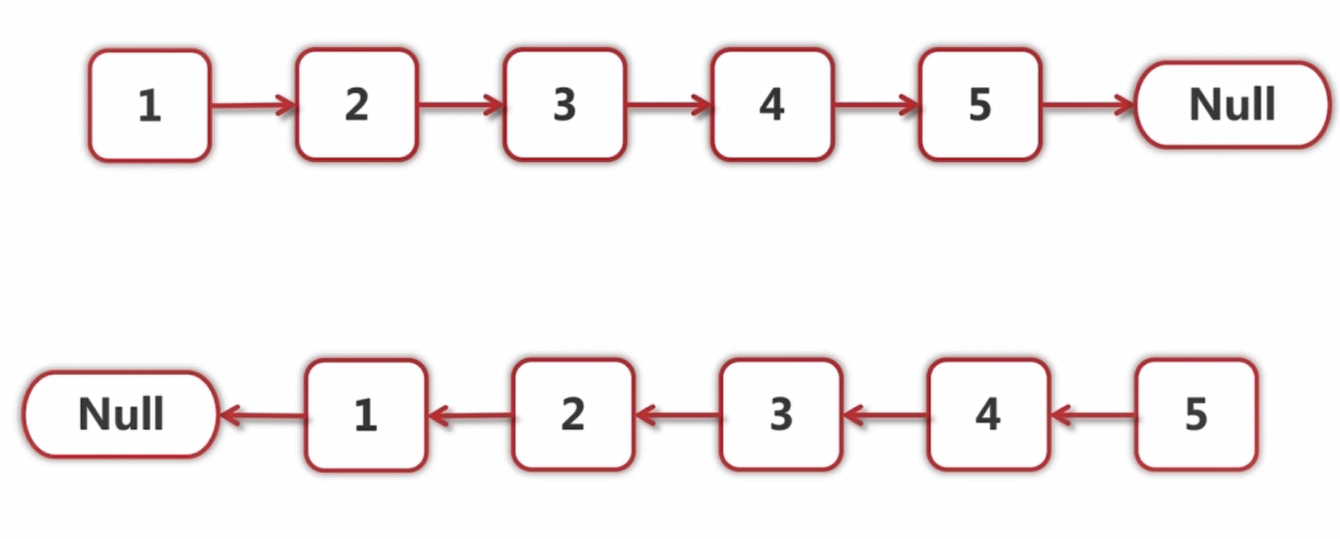
我们跟上面一样考虑，考虑一般的情况，那就是1后面的所有元素已经全部反转好了，初始状态为：

此时假定后面全部反转好了：

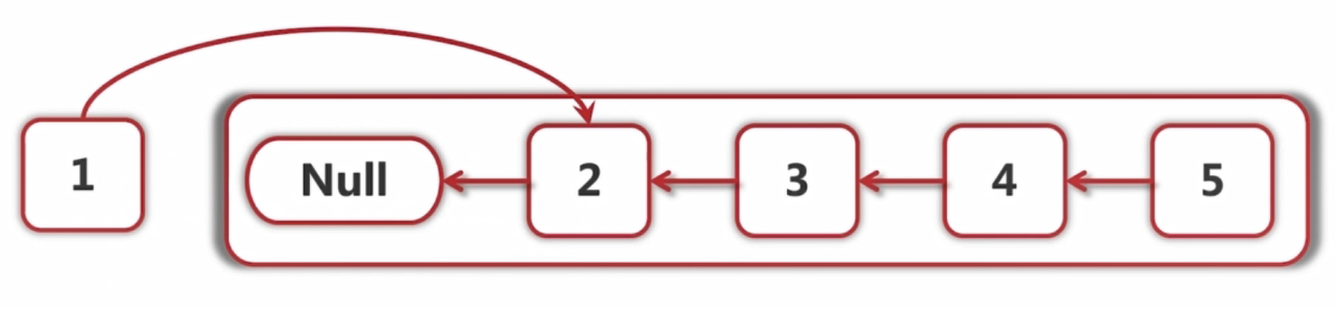
下面只需要将2指向1，并且1指向null即可：

public Node reverseLinkedList(Node head){
    if(head == null || head.getNext() == null){
        return head;
    }
    Node newHead = reverseLinkedList(head.getNext());
    head.getNext().setNext(head);
    head.setNext(null);
    return newHead;
}

六、递归存在的问题

比如计算斐波那契数列：

public int fib(int index){
	if(index==1||index==2){
		return 1;
	}else{
		return fib(index-1)+fib(index-2);
	}
}

在这个递归里做了冗余的工作，如图，我们在f4里面已经计算了f2，可是f3里有同样计算了f2，以此类推那些冗余的工作，在数值比较小的情况下，计算机还是可以接受的。但是，当求解的数值比较大，它是成指数级增长的，所以不要再递归中做重复的工作。

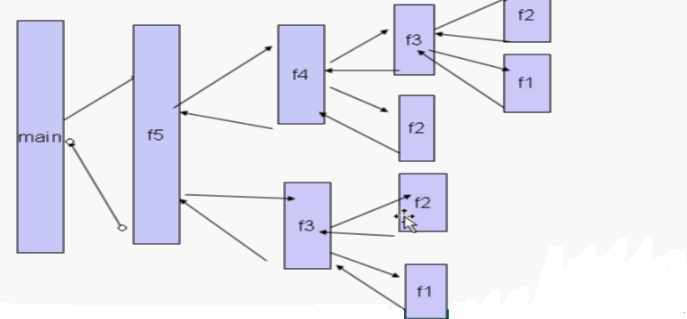
下一节通过经典得汉诺塔问题再来探讨一下递归的思想。