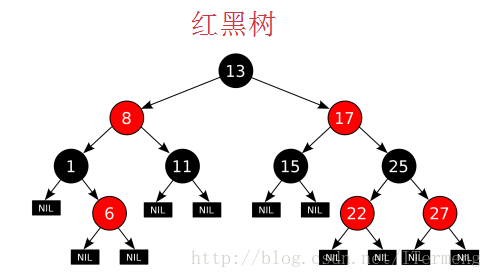
基础算法5-二分搜索树
数据结构中有很多树的结构,其中包括二叉树、二叉搜索树、2-3树、红黑树等等。普通的二叉树其实没什么好讲的,就是最多只有两个孩子的树,而二叉搜索树赋予了它一些额外的条件,使得它有了使用的价值,例如根据它的性质,那么中序遍历出来的结果恰好就是有序的结果,故本文着重说明二叉搜索树。
一、二叉树
二叉树是数据结构中一种重要的数据结构,也是树表家族最为基础的结构。它本身对里面的数据是没有说明要求的,只是个数要满足二叉树的每个结点至多只有二棵子树(不存在度大于2的结点),二叉树的子树有左右之分,次序不能颠倒。二叉树的第i层至多有2的(i-1)次方个结点;深度为k的二叉树至多有2的k次方-1个结点;
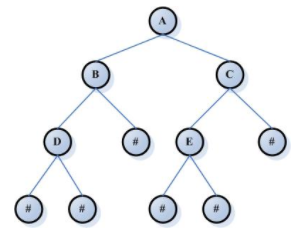
二、满二叉树和完全二叉树
一张图就可以看出它们的区别了:
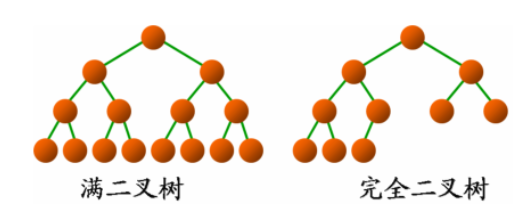
三、二叉搜索树概念
二叉查找树定义:又称为是二叉排序树(Binary Sort Tree)或二叉搜索树,不需要是一棵完全二叉树。具有以下性质:
- 若左子树不空,则左子树上所有结点的值均小于它的根结点的值;
- 若右子树不空,则右子树上所有结点的值均大于或等于它的根结点的值;
- 左、右子树也分别为二叉排序树;
- 没有键值相等的节点。
二叉查找树的性质:对二叉查找树进行中序遍历,即可得到有序的数列。
二叉查找树的时间复杂度:它和二分查找一样,插入和查找的时间复杂度均为O(logn),但是在最坏的情况下仍然会有O(n)的时间复杂度。原因在于插入和删除元素的时候,树没有保持平衡。我们追求的是在最坏的情况下仍然有较好的时间复杂度,这就是平衡查找树设计的初衷。
二叉查找树的高度决定了二叉查找树的查找效率。
四、树的定义
就是说如果我要定义一个二叉树,那么这个Node如何定义呢?其实很简单,无非就是left,right,val这三个变量而已,也有可能是key和value这种类型,这个定义是在《算法4》上看到的,二叉搜索树判断大小的依据就是这个key.不必对这个纠结.
1 | //二分搜索树 |
五、插入新节点
查看以下动画演示了解插入新节点的算法思想:(其插入过程充分利用了二分搜索树的特性)
例如待插入数据60,首先与根元素41比较,大于根元素,则与其右孩子再进行比较,大于58由于58无右孩子,则60为58的右孩子,过程结束。(注意其递归过程)

判断node节点是否为空,为空则创建节点并将其返回( 判断递归到底的情况)。
若不为空,则继续判断根元素的key值是否等于根元素的key值:若相等则直接更新value值即可。若不相等,则根据其大小比较在左孩子或右孩子部分继续递归直至找到合适位置为止。、
代码实现(递归实现):
1 | // 向二分搜索树中插入一个新的(key, value)数据对 |
六、二分搜索树的查找
1 | // 查看二分搜索树中是否存在键key |
七、二分搜索树的遍历
这块内容其实我想删除的,但是吧,这一段对树的前中后序遍历的动态图是非常不错的,对理解树的遍历是非常有利的,所以保留在这里。下面进入正文。
遍历分为前序遍历、中序遍历以及后序遍历三种,如何理解其遍历顺序呢?
对于每个节点而言,可能会有左、右两个孩子,所以分成下图中3个点,每次递归过程中会经过这3个点。
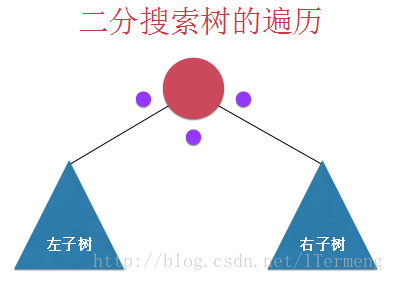
前序遍历:先访问当前节点,再依次递归访问左右子树
中序遍历:先递归访问左子树,再访问自身,再递归访问右子树
后续遍历:先递归访问左右子树,再访问自身节点
下面分别来看看是如何遍历的。
7.1 前序遍历

我们注意看,先找到28的第一个点,然后将28返回,下面看有没有左儿子,有就先来到左儿子的节点,然后将16弹出…
最终的打印结果:
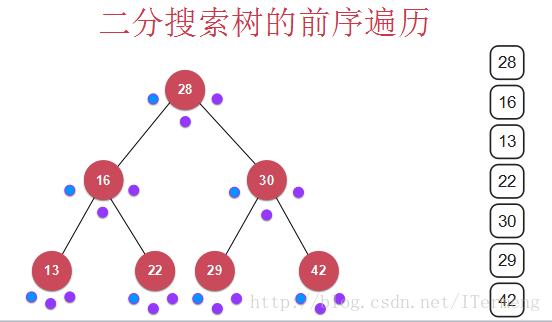
7.2 中序遍历

最终的打印结果:
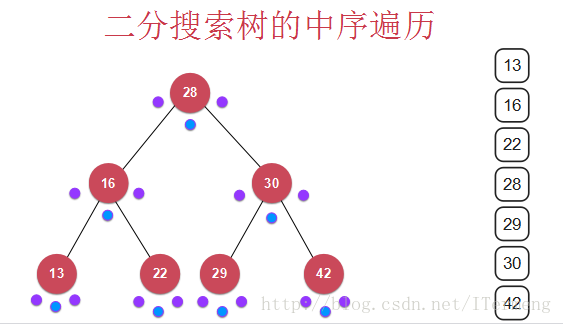
7.3 后序遍历

最终打印结果:
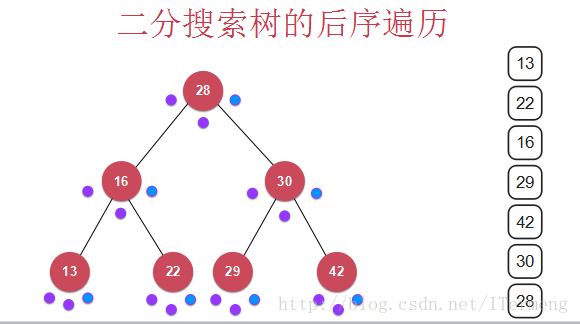
7.4 递归代码实现
1 | // 对以node为根的二叉搜索树进行前序遍历, 递归算法 |
针对非递归的写法,推荐用第二篇文章中说明的方式,那种方式具有较好的通用性。当然了,此时应该认识到学好递归的重要性了。
八、层序遍历
8.1 算法思想
层序遍历即一层一层地向下遍历,查看以下动画:
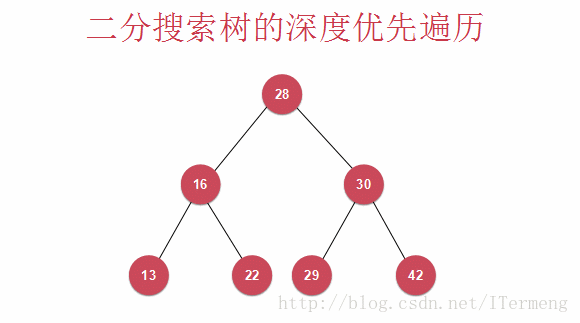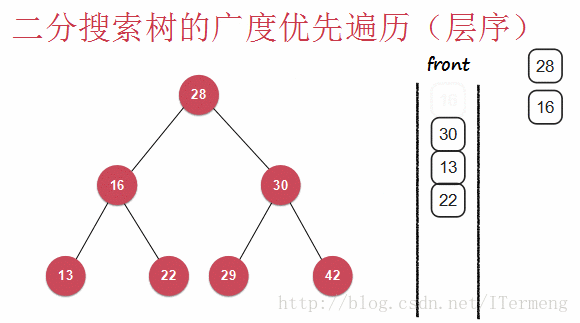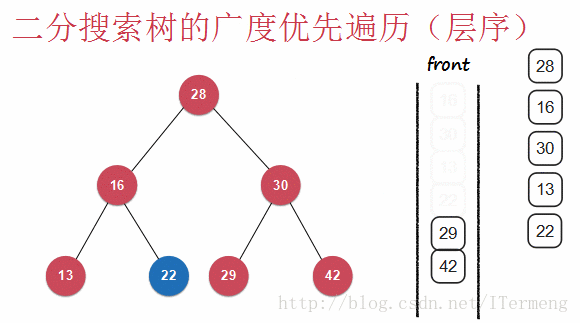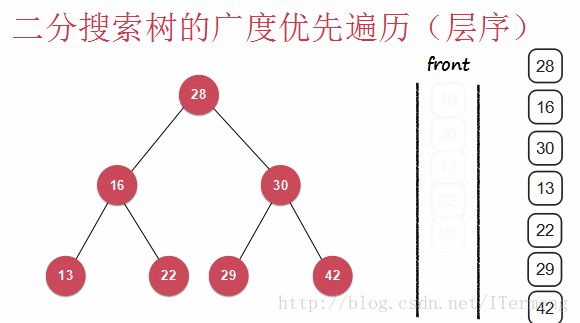
查看以上动画,实现其过程需要引入先进先出的“队列”数据结构,首先将28入队,第一层遍历完毕,可进行操作,将28出队并打印。遍历第二层16、30依次入队,再出队进行打印操作,依次类推。
8.2 代码实现
1 | // 二分搜索树的层序遍历 |
九、局限性来源
它的局限性来源于哪?注意其二分搜索树的创建,如下图所示,同样的数据,可以对应不同的二分搜索树。
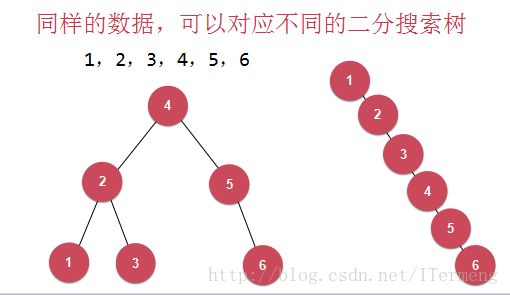
如上图,第一种创建情况可能是大部分人心中设想,但是第二种情况也是符合二分搜索树的特征,如此一来,二分搜索树可能退化成链表。二分搜索树的查找过程是与其高度相关,此时高度为n,时间复杂度为O(n^2)。
十、初识红黑树
其实二分搜索树的性能总体而言还是十分优异的,它所有的有关操作时间复杂度为O(n),出现以上情况的概率很小,但如果创建时其数据都是有序的,那么就会令人担忧了。也许你会想到快速排序中也有此问题,不过它通过随机获取标志点的方法解决了此问题。
所以类似以上解决办法,将其顺序打乱再插入到二分搜索树即可?这是一个解决办法,但是需要一开始获取所有数据,其实这些数据是慢慢流入系统的,所以在创建其过程中才会发现数据是否几乎有序。
为了解决此问题,可以改造二叉树的实现,使得其无法退化成链表—–平衡二叉树,它有左右两棵子树,并且其高度差不会超过1,因此可以保证其高度一定是 logn 级别的,此概念的经典实现就是红黑树。