基础算法6-关于二叉树的经典面试题分析

掌握对树的基本操作是很重要的，这里所谓的操作是指对树的遍历，以及对树的构造等等。下面通过一些题目来好好研究研究。由于篇幅、时间以及精力有限，本文着重提取两种题型进行分析，都是高频面试问题。

问题1

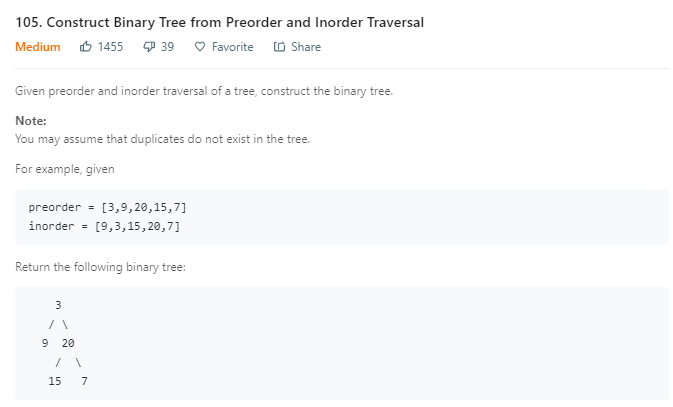
这是一道比较常见的题目，虽然难度是medium，但是也没有那么难，这个题目主要是要求我们根据前序遍历和中序遍历构造出整棵树。

基本的思路是：

也就是说，前序遍历的第一个元素必然是整棵树的头节点，那么我在中序遍历找到头节点的位置后，就可以根据中序遍历的特点，前面的都是左子树，后面的都是右子树。找到了这一个，下面就让计算机递归去找，所以问题的关键就是第一步的缩小范围。无需关心构造树的细节。

我的解题方案是：

class Solution {
    public TreeNode buildTree(int[] preorder, int[] inorder) {
        //6.递归的停止条件，最后考虑，先考虑下面的一般情况
        if(preorder.length == 0){
            return null;
        }
        
        //1.根据前序遍历的结果，第一个元素就是树的root
        int rootVal = preorder[0];
        
        //2.根据root的值去inorder中去找，题目规定这个序列是没有重复元素的
        int rootIndex = 0;
        for(int i=0;i<inorder.length;i++){
            if(inorder[i] == rootVal){
                rootIndex = i;
                break;
            }
        
        }
        //3.找到了之后，我们就可以确定root的左子树和右子树的所有元素了
        TreeNode root = new TreeNode(rootVal);
        
        //4.下面就交给计算机了，我们只要考虑第一次的缩小规模，即root的左子树是什么范围，递归下去，相信它一定可以给我们一个正确的root的左子树
        //这个范围的确定也是很简单的，根据前序遍历和中序遍历的关系就可以获得
        //不过额外需要注意的是Arrays.copyOfRange是一个[)的结果集，需要注意以下边界
        root.left = buildTree(Arrays.copyOfRange(preorder,1,1+rootIndex),Arrays.copyOfRange(inorder,0,rootIndex));
        //递归下去，相信它一定可以给我们一个正确的root的右子树
        root.right = buildTree(Arrays.copyOfRange(preorder,1+rootIndex,preorder.length),Arrays.copyOfRange(inorder,rootIndex+1,inorder.length));
        
        //5.返回root，构造完毕
        return root;
    }
}

问题2

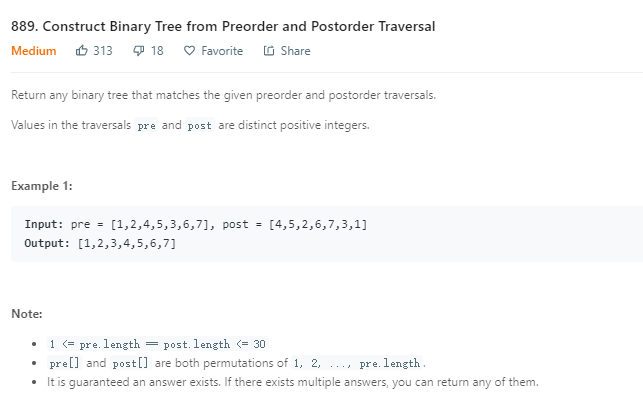
根据前序和后序构建的二叉树不唯一，理由是前序与后序都没有明确规定节点间的父子关系，例如下图所示：

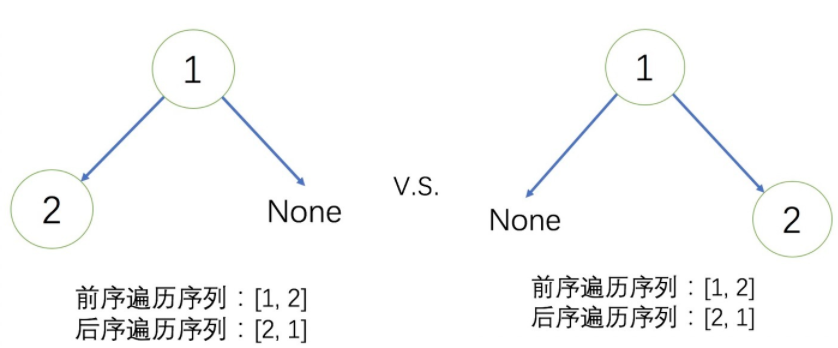
本题比较人性化，要求只要输出其中一种可能性即可。还是可以根据一般的思路，采用递归思想，对于每一个先序序列，划分出对应的根节点、左子树、右子树范围即可自上而下构建出二叉树。

例如对于上例中的先序序列[1,2,4,5,3,6,7]，第一个节点一定为根节点，第2到第i个节点为左子树，第i+1到最后一个节点为右子树，那么问题就可以简化为：如何确定左右子树分界点？

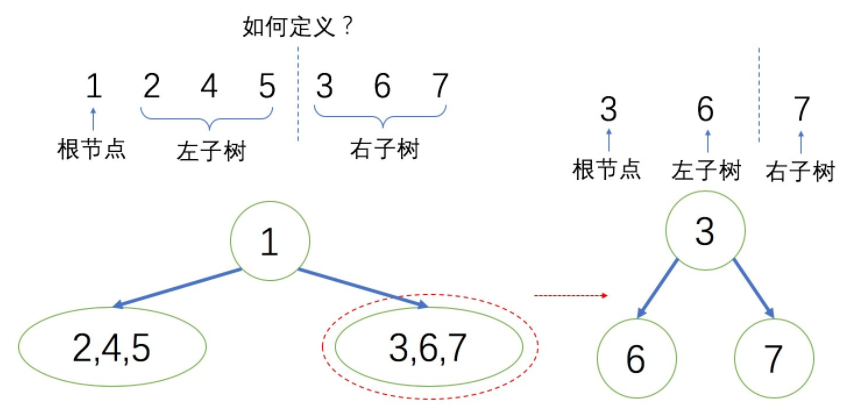
对于这个简化过后的问题，从后序遍历序列上很容易得到答案：

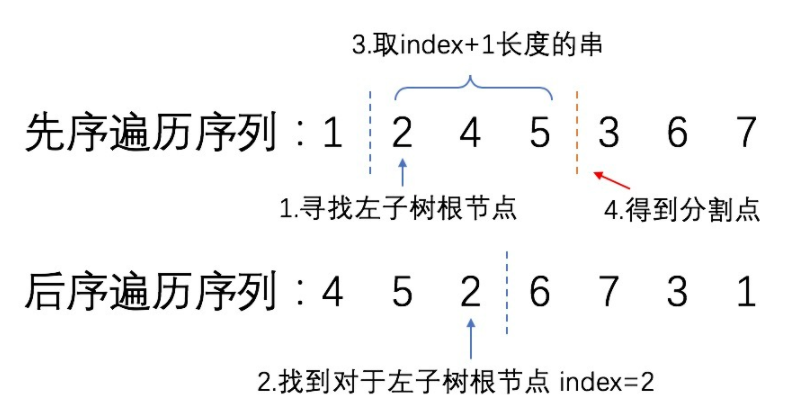
根据上图的思路，就可以写代码啦：

class Solution {
    public TreeNode constructFromPrePost(int[] pre, int[] post) {
        //
        if(pre.length == 0){
            return null;
        }
        //数组还有元素，则取出第一个元素作为root
        TreeNode root = new TreeNode(pre[0]);
        
        //数组长度为1 的时候直接返回即可
        if(pre.length == 1){
            return new TreeNode(pre[0]);
        }

        //找到左子树根节点在后序遍历中的位置，找到之后，元素前面的都是左子树元素，后面除了最后一个元素都是右子树元素
        int leftRootIndex = 0;
        int leftRootVal = pre[1];
        for(int i=0;i<post.length;i++){
            if(post[i] == leftRootVal){
                leftRootIndex = i;
                break;
            }
        }
        
       
        //递归构造
        root.left = constructFromPrePost(Arrays.copyOfRange(pre,1,leftRootIndex+2),
                                        Arrays.copyOfRange(post,0,leftRootIndex+1));
        
        root.right = constructFromPrePost(Arrays.copyOfRange(pre,leftRootIndex+2,pre.length),
                                         Arrays.copyOfRange(post,leftRootIndex+1,post.length-1));
        
        return root;
    }
}

问题3

到现在为止，我们对于中序排序的规则已经很熟悉，下面图示:

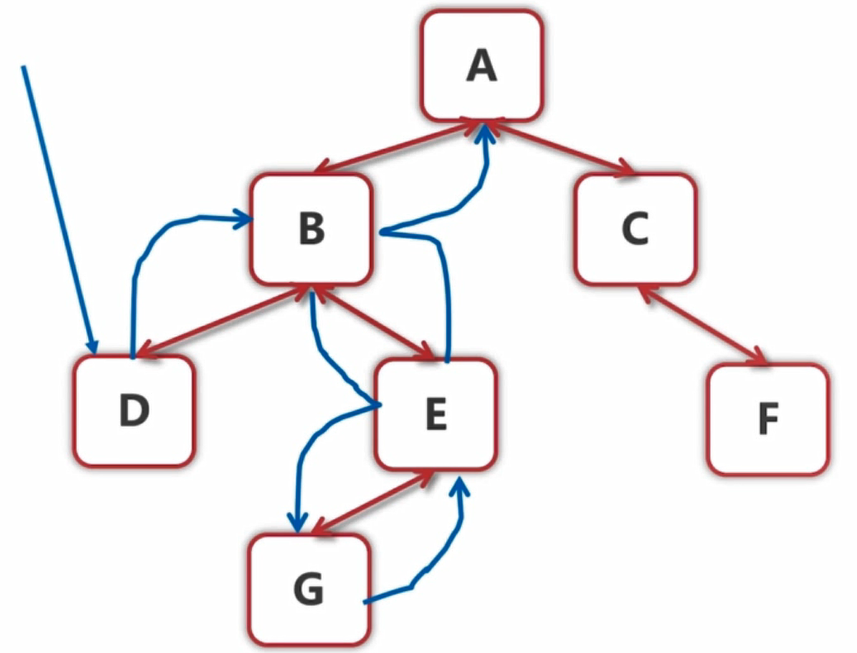
我们从这个图上可以看到，找下一个节点是可以分为几种情况的。

第一种情况，就是一个节点有右子树。比如要求节点B的下一个节点，其实是找到它的右子树的最左孩子，就是G节点。

第二种情况，就是一个节点没有右子树，此时又可以分为两种情况。

对于G这个节点来说，没有右子节点了，它的父亲节点是E，G是E的左子节点，即E的左子节点是G，那么G的下一个节点就是E。

对于E这个节点来说，也没有右子节点，它的父亲节点是B，此时E是B的右子节点，根据实际情况来说，E的下一个节点绝对不是B，因为E是B的右子节点，根据中序遍历的规则，此时肯定是先遍历B再遍历E，所以B肯定在E的前面，而不是后面，所以我们还需要再往上找父亲节点，此时B的父亲节点为A，B为A的左子节点，此时根据实际情况，A就是我们要找的E的下一个节点。

所以，对于一个没有右子节点的节点来说，只需要判断它有没有父节点并且是不是父节点的左子节点，是的话，就找到了，不是则要不断地向上找。

如果一直找到根还是找不到，像节点F，那就返回null，因为实际上F节点就是中序遍历的最后一个节点，没有所谓的下一个节点了。

将上面所述转换为图示为：

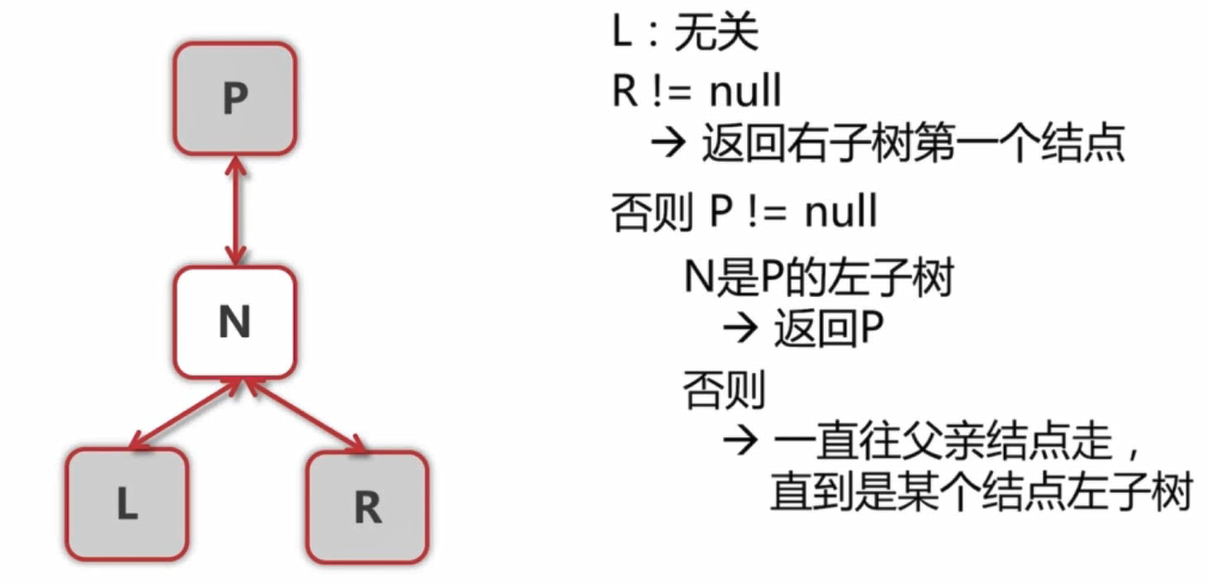
总之，我们不关心当前节点的左子节点，因为它不在我们的考虑范围内，它必定出现在当前节点的前面。

我们主要就是考虑有没有右子节点，或者没有右子节点的话就考虑父亲节点。有右子节点比较简单，一直找最左边的子节点即可。但是没有右子节点的时候，就需要去查询父亲节点了。理解了这些，程序也就呼之欲出了：

public class Solution {
    public TreeLinkNode GetNext(TreeLinkNode pNode)
    {
        if(pNode == null){
            return null;
        } 
        
        //1.判断当前节点是否有右子节点，有则去里面找
        if(pNode.right != null){
            return firstInRightTree(pNode);
        //2.没有右子节点，就需要去父节点找
        }else{
            //3.直到找到符合条件的父节点为止，跳出循环时pNode的父节点符合条件，这个父节点就是我们要的东西
            while(pNode.next != null && pNode.next.left != pNode){
                pNode = pNode.next;
            }
            return pNode.next;
        }
    }
    
    //到右子树中找符合条件的，显然就是找最最最左边的子节点即可
    private TreeLinkNode firstInRightTree(TreeLinkNode pNode){
        TreeLinkNode curr = pNode.right;
        while(curr.left != null){
            curr = curr.left;
        }
        return curr;
    }
}

这里对比较常见的树的一些算法题进行了分析，关于树的题目还有很多，并且很多重要的题目也还每设计到，后面有时间整理一下leetcode上比较经典的二叉树的算法题。