从本文开始就要介绍O(nlogn)复杂度级别的排序算法了，首先登场的是归并排序，这个排序可以解决一些问题，会在文章的后面给出，并且是一个经典的分治思想，即先分隔再合并，将复杂的大问题瓦解为小问题，将若干小问题解决了之后大问题也就迎刃而解了。下面我们来学习一下归并排序的基本原理。

1. 原理

归并排序（MERGE-SORT）是利用归并的思想实现的排序方法，该算法采用经典的分治（divide-and-conquer）策略（分治法将问题分(divide)成一些小的问题然后递归求解，而治(conquer)的阶段则将分的阶段得到的各答案"修补"在一起，即分而治之)。

复杂度为(nlogN),这里采用自顶向下和递归来完成的。

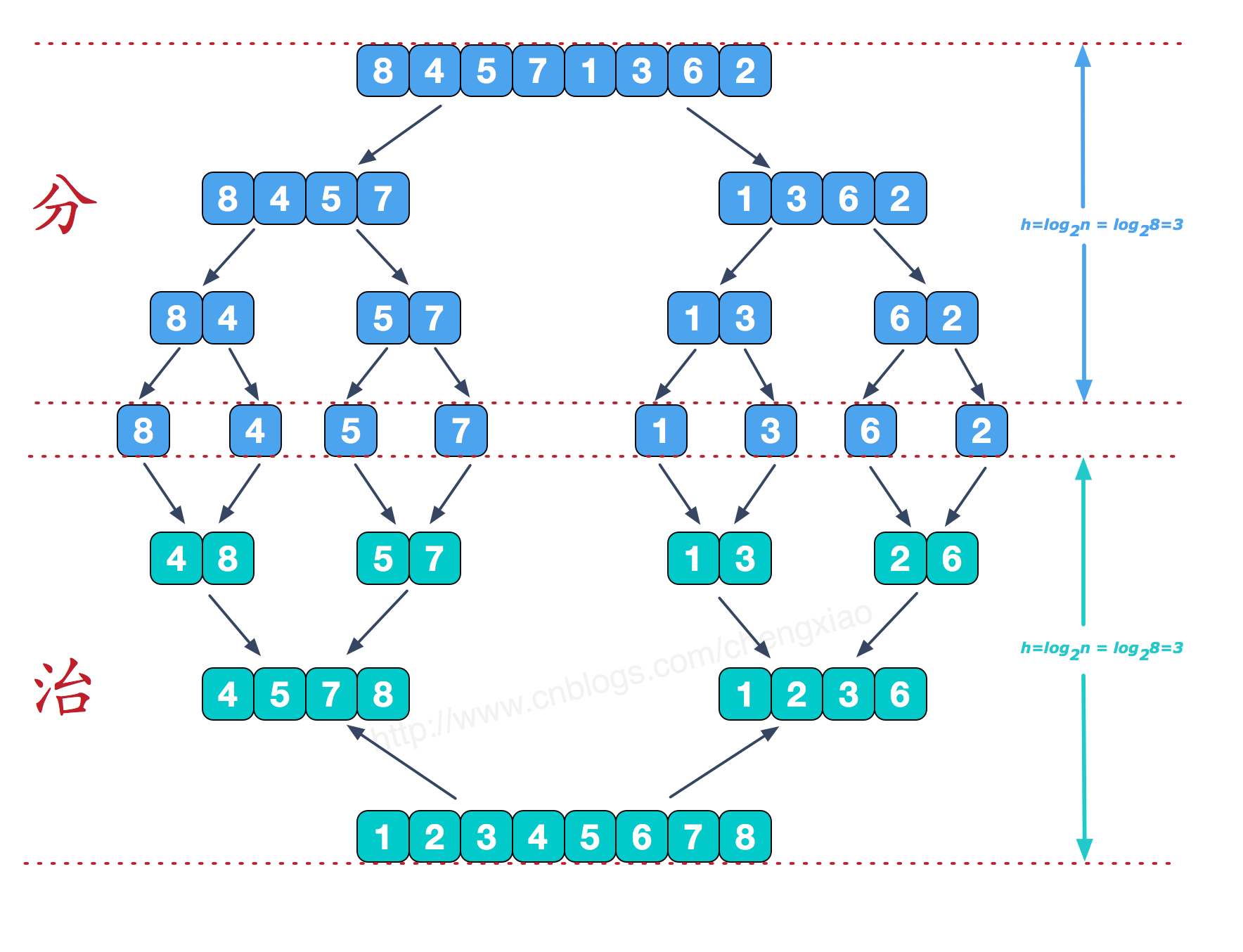
image

归并排序的原理是，先把待排序序列分为若干个子序列，每个子序列是有序的。然后再把有序子序列合并为整体有序序列。

归并的前提是先把要排序的序列分为若干个字序列，然后才归并。在拆分数列的时候，就要用到拆分，直到不能再拆为止。

如一个数列{9,8,7,6,5,4,3,2,1}

先分成{9,8,7,6,5}和{4,3,2,1}

然后再分成{9,8,7}和{6,5}和{4,3}和{2,1}

然后再分{9,8}、{6}、{5}、{4}、{3}、{2}、{1}

然后再合并起来，小在的前面，大的在后面，没有比较的在后面填充数列。

具体如何合并的呢？下面展示的最后的一步合并过程：

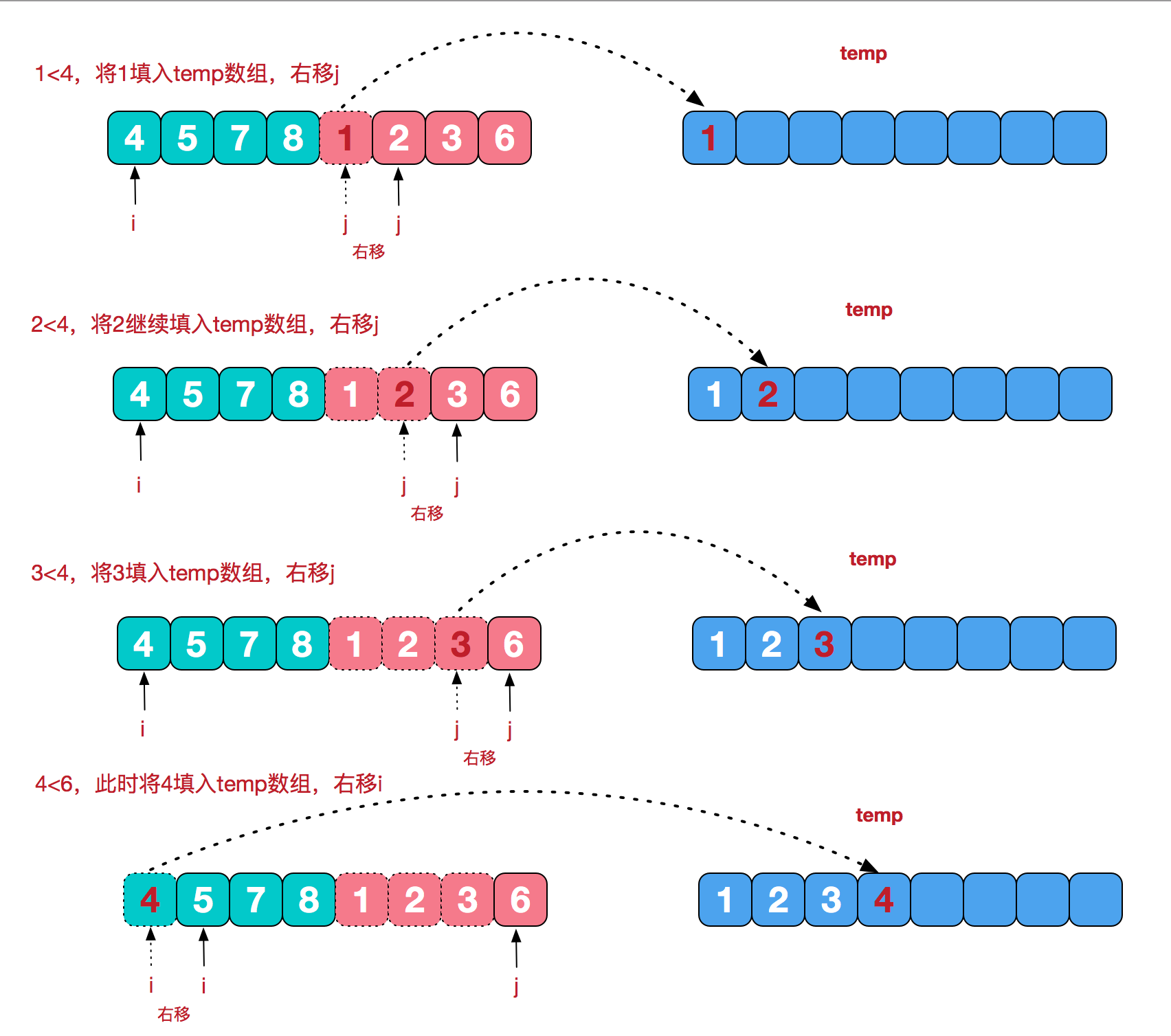
image

我们注意到，归并排序是需要额外的空间来辅助的。动态图为：

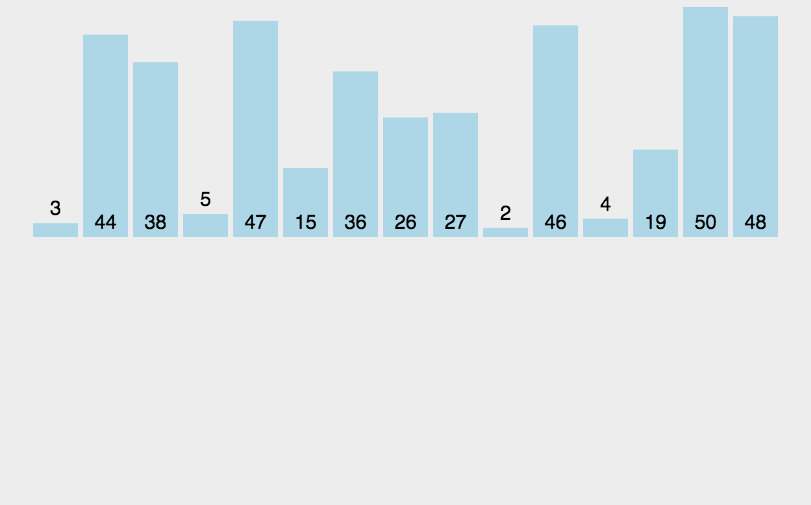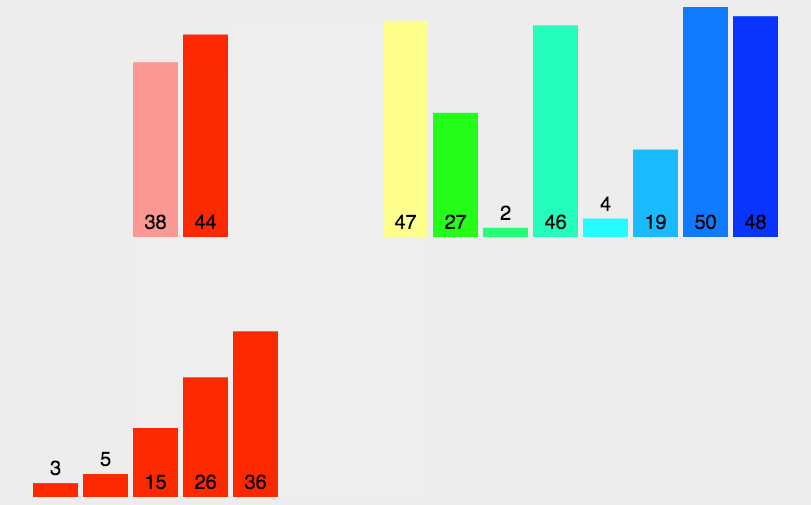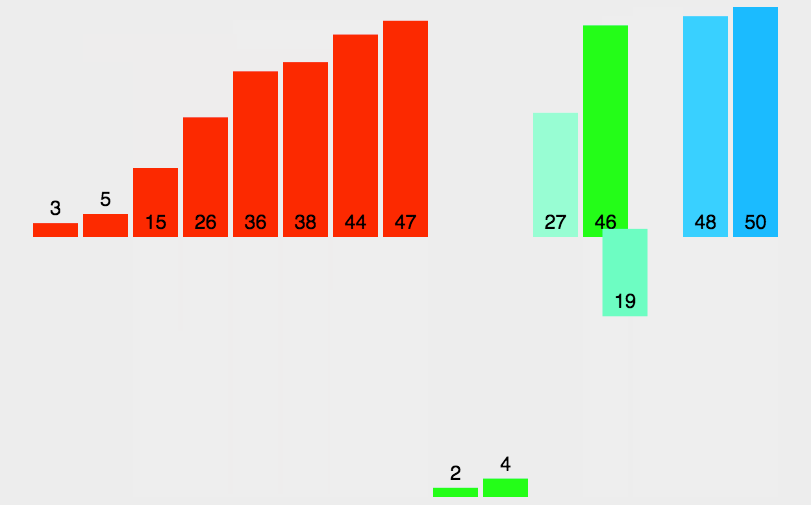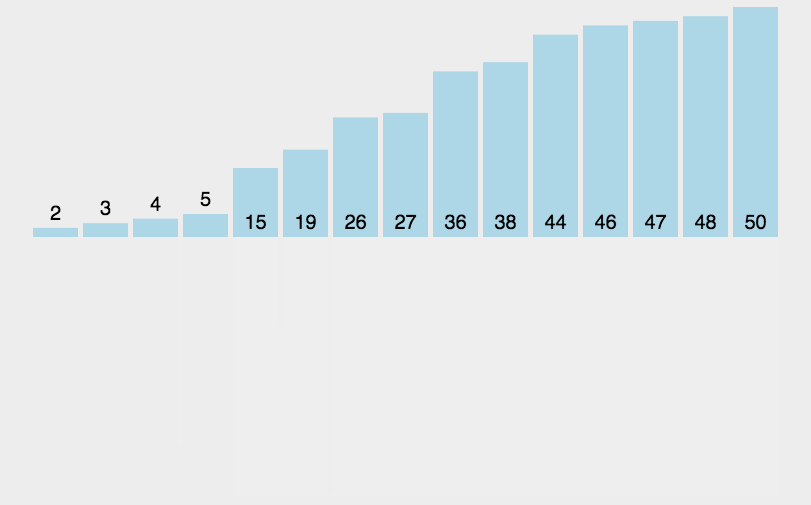
image

2. 代码

2.1 左右分开
1
2
3
4
5
6
7
8
9
10
11
12
13
public static void sort(int[] a, int low, int high) {
    //int mid = (low + high) / 2;
	int mid = low + (high - low)/2;
    if (low < high) {
        //左边归并排序，使得左子序列有序
    	sort(a, low, mid);
        //右边归并排序，使得右子序列有序
    	sort(a, mid + 1, high);
        //将两个有序子数组合并操作
        merge(a, low, mid, high);
    }

}
2.2 合并过程
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
public static void merge(int[] a, int low, int mid, int high) {
    int[] temp = new int[high - low + 1];
    int i = low;// 左指针
    int j = mid + 1;// 右指针
    int k = 0;//临时指针
    // 把较小的数先移到新数组中
    while (i <= mid && j <= high) {
        if (a[i] < a[j]) {
            temp[k++] = a[i++];
        } else {
            temp[k++] = a[j++];
        }
    }
    // 把左边剩余的数移入数组
    while (i <= mid) {
        temp[k++] = a[i++];
    }
    // 把右边边剩余的数移入数组
    while (j <= high) {
        temp[k++] = a[j++];
    }
    // 把新数组中的数覆盖原数组
    for (int k2 = 0; k2 < temp.length; k2++) {
        a[k2 + low] = temp[k2];
    }
}

对于它的理解，一句话就是先对半分，分到不能分为止，然后再倒过来将卡擦分开的两组数进行比较合并成有序序列，最终逐渐合并成有序序列。

3. 归并排序应用1–小和问题

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
/**
 * 归并排序的应用
 *
 *  在一个数组中，每一个数左边比当前数小的数累加起来，叫做这个数组的小和。求一个数组的小和。
 *
 *  例子：
 *  [1,3,4,2,5]
 *  1左边比1小的数，没有；
 *  3左边比3小的数，1；
 *  4左边比4小的数，1、3；
 *  2左边比2小的数，1；
 *  5左边比5小的数，1、3、4、2；
 *  所以小和为1+1+3+1+1+3+4+2=16
 */
public class MergeSortApply1 {
    public static void main(String[] args) {
        int[] arr= {1,3,4,2,5};
        System.out.println(merge_sort(arr));
    }


    public static int merge_sort(int[] arr){
        if(arr == null || arr.length < 2){
            return 0;
        }
        return sortProcess(arr,0,arr.length-1);
    }

    private static int sortProcess(int[] arr, int low, int high) {
        if(low == high){
            return 0;
        }

        int mid = low + (high-low)/2;

        return sortProcess(arr,low,mid) +
                sortProcess(arr,mid+1,high) +
                  merge(arr,low,mid,high);
}

    private static int merge(int[] arr, int low, int mid, int high) {
        int[] help = new int[high-low+1];
        int k = 0;
        int p1 = low;
        int p2 = mid+1;
        int count = 0;
        while(p1 <= mid && p2 <= high){
            //核心的是增加这一句，当发现arr[p1] < arr[p2]时
            //那么p2后面的数必然都大于它，所以这一次合并过程中
            //p1位置比(high-p2+1)这些位置都小，那么针对这个p1位置的数字，一次性全部累计起来即可
            count += arr[p1] < arr[p2] ? (high-p2+1)*arr[p1] : 0;
            help[k++] = arr[p1] < arr[p2] ? arr[p1++] : arr[p2++];
        }

        while(p1 <= mid){
            help[k++] = arr[p1++];
        }
        while(p2 <= high){
            help[k++] = arr[p2++];
        }

        for(int ii=0;ii<help.length;ii++){
            arr[ii+low] = help[ii];
        }

        return count;
    }

}

4. 归并排序应用2–逆序对问题

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
/**
 * 归并排序的应用
 *
 *  在一个数组中，左边的数如果比右边的数大，则折两个数构成一个逆序对，请打印所有逆序对的数量。
 */
public class MergeSortApply2 {
    public static void main(String[] args) {
        int[] arr= {1,2,3,4,5,6,7,0};
        System.out.println(merge_sort(arr));
    }


    public static int merge_sort(int[] arr){
        if(arr == null || arr.length < 2){
            return 0;
        }
        return sortProcess(arr,0,arr.length-1);
    }

    private static int sortProcess(int[] arr, int low, int high) {
        if(low == high){
            return 0;
        }

        int mid = low + (high-low)/2;

        return sortProcess(arr,low,mid) +
                sortProcess(arr,mid+1,high) +
                  merge(arr,low,mid,high);
}

    private static int merge(int[] arr, int low, int mid, int high) {
        int[] help = new int[high-low+1];
        int k = 0;
        int p1 = low;
        int p2 = mid+1;
        int count = 0;
        while(p1 <= mid && p2 <= high){
            //归并的过程中发现前面大于后面的话就算一组
            count += arr[p1] > arr[p2] ? (high-p2+1) : 0;
            help[k++] = arr[p1] < arr[p2] ? arr[p1++] : arr[p2++];
        }

        while(p1 <= mid){
            help[k++] = arr[p1++];
        }
        while(p2 <= high){
            help[k++] = arr[p2++];
        }

        for(int ii=0;ii<help.length;ii++){
            arr[ii+low] = help[ii];
        }

        return count;
    }

}