堆排序的重要性在于它涉及到二叉堆这个数据结构，面试中曾经被问过堆这个数据结构，那么堆其实是一个完全二叉树，它里面含有好几种类型的堆，其中我们比较关注的是二叉堆，它分为大顶堆和小顶堆，是非常常用的一种数据结构。所以我觉得面试中问到堆这个数据结构的时候可以往二叉堆上进行靠拢，然后回答问题。

1. 前言

在学习堆排序之前，有必要把一些数据结构方面的知识理一下，要不然会有点乱。

首先看一下一个大的分类：

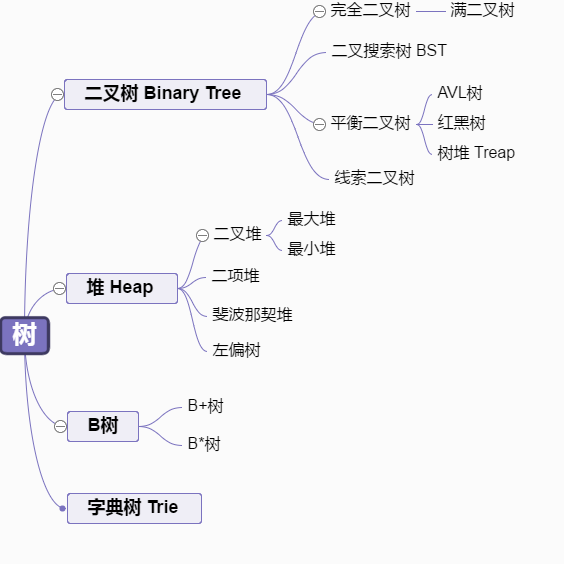
image

因此堆是一种特殊的树，并且是特殊的完全二叉树。对于堆排序中的堆通常是指二叉堆。二叉堆分为大根堆和小根堆。其中每个节点的值小于等于其左、右孩子的值，这样的堆称为小根堆；其中每个节点的值大于等于其左、右孩子的值，这样的堆称为大根堆；这里注意二叉堆和二叉搜索树的区别。

那么理清这个关系之后，我们知道了，我们主要的研究对象是二叉堆这个数据结构。

2. 二叉堆的结构

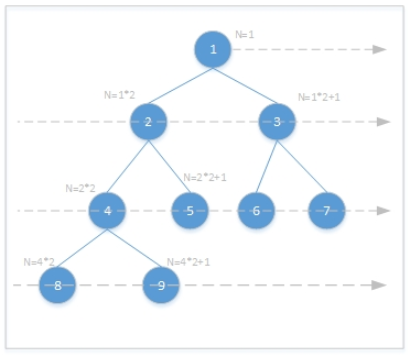
回顾一下完全二叉树的定义。

如下图，每一层都是从左向右摆放节点，每个节点都是摆满两个子节点后才向右移动到下一个节点，一层摆满后向下移动一层，直到摆放完所有数字。这样得到的二叉树就是完全二叉树，中间有任何缺失的节点就不能称为完全二叉树。

image

二叉堆是一种完全二叉树，他们的区别是：

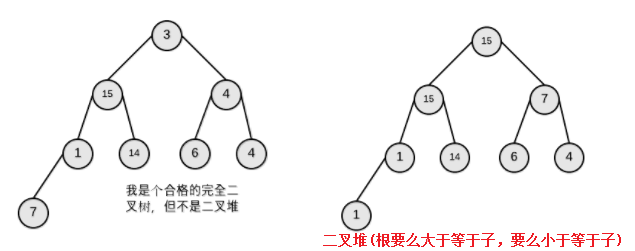
二叉堆与完全二叉树

二叉堆是一颗完全二叉树，完全二叉树有一个非常重要的性质：即完全二叉树只用数组而不需要指针就可以表示。优势在于数组表示的话内存是紧凑排列的，不会有太多的内存碎片，并且数组对于随机访问是很快的，基于数组下标即可。

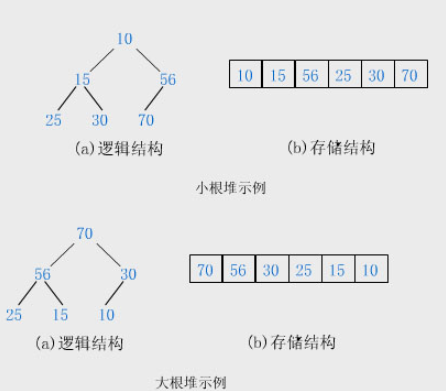
堆用数组表示

3. 二叉堆与优先队列

什么是优先队列，队列我们是比较熟悉的，是一种先进先出的数据结构，在优先队列中，出队的顺序与入队的顺序无关了，而是与优先级有关。即优先级越高，越早出队。

优先队列到底有什么实际应用呢？比如一个电商网站搞特卖或抢购，用户登录下单提交后，考虑这个时间段用户访问下单提交量很大，通常表单提交到服务器后端后，后端程序一般不直接进行扣库存处理，将请求放到队列列，异步消费处理，用普通队列是FIFO的，这里有个需求是，用户会员级别高的，可以优先抢购到商品，可能这个时间段的级别较高的会员用户下单时间在普通用户之后，这个时候使用优先队列代替普通队列，基本能满足我们的需求。

优先队列就是依靠二叉堆来实现的。优先队列需要支持两种操作：

  • 删除最小（最大）元素
  • 插入元素

为什么要用堆来实现优先队列？

  • 优先队列所需要实现的两种操作，不同于队列和栈，它需要一个有序的元素序列，但不要求全部有序，只需要从这些元素中找到最大（或最小）的一个元素。而堆刚好满足这个条件。
  • 队列，栈都是用数组或者链表来实现的，针对优先队列，用数组和链表实现也是可以的，在队列较小，大量使用两种操作之一时，或者所操作的元素的顺序已知时，用数组和链表十分有用，但是，在最坏的情况下，优先队列用这两张方法实现所需的时间却是线性的。而用堆在最坏情况下的时间则是对数级别。

由于我们比较关注的是立即拿到最大或者最小的元素，然后高效地删除和插入。这些都依赖于堆的内部算法实现，下面我们就来看看大顶堆为例的插入和删除操作原理。

4. 堆的算法

我们用N+1长度的数组来表示一个大小为N的堆，我们不会使用[0],堆元素会被保存于[1]-[N-1]中。

4.1 大顶堆的插入(上浮)

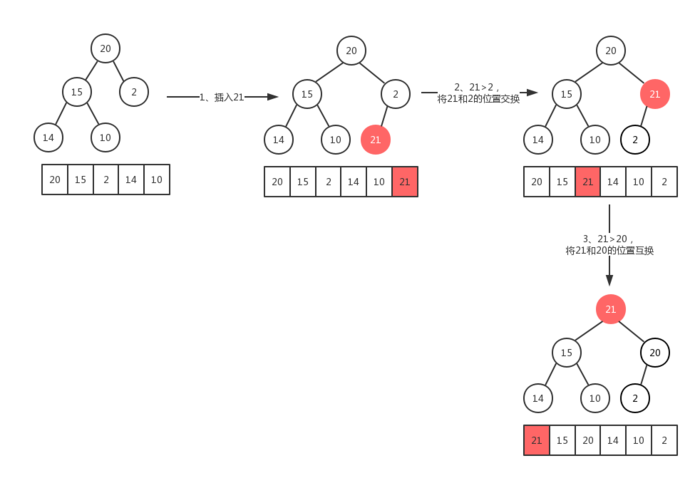
image

1
2
3
4
5
6
7
8
9
/*
 * k:当前插入元素的位置，相应地k/2就是其父结点的位置
 */
private void swim(int k){
	while(k>1 && less(k/2,k)){
		swap(k/2,k);
		k = k/2;
	}
}
4.2 大顶堆的删除

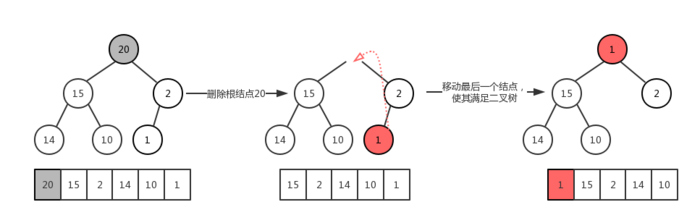
image

1
2
3
4
//伪代码
1. 获取根结点
2. 将根结点与最后一个结点交换
3. 恢复堆的有序性...

显然现在看来该二叉树虽然是一个完全二叉树，但是它并不符合最大堆的相关定义，我们的目的是要在删除完成之后，该完全二叉树依然是最大堆。因此就需要我们来做一些相关的操作！

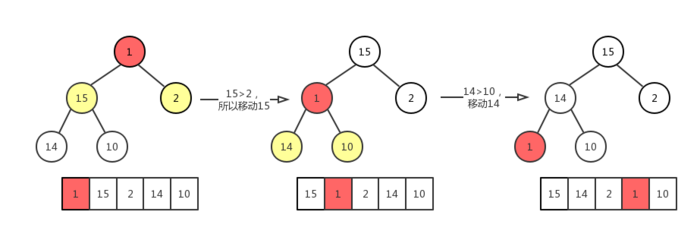
image

1
2
3
4
5
6
7
8
9
10
11
12
13
14
/*
 * k:当前被删除元素的位置(若删除根节点,则k=1)，相应地2*k就是其左子结点的位置
 */
private void sink(int k){
	while(2*k < N){
		int j = 2 * k;
		if(j < N && less(j,j+1))
			j++;
		if(!less(k,j))
			break;
		swap(k,j);
		k = j;
	}
}

5. 堆排

在了解了堆的基本操作之后，我们将目标先转到堆排序上，这才是本章研究的重点。

时间复杂度为O(logN)，额外空间复杂度为O(1);

我们知道，数组可以对应到一个完全二叉树。

堆:大根堆和小根堆。堆就是一个完全二叉树。

大根堆：完全二叉树中任何一个子树的最大值就是其头部节点对应的值。

那么，数组已经是一个完全二叉树，而下面的任务就是：将一个数组变成大根堆。

构建一个大根堆的复杂度是log1+log2+…+logi = O(N)

第一次构建完大根堆之后，还不是有序的。堆排序的主要思路是：每次将最后一个数与第一个数交换，就是完全二叉树的最后一个数与根节点进行交换。由于根节点已经是最大的数，所以我们就可以不要再管它。我们再将0~n-1下标的所有数进行调整，也调整为大顶堆，然后重复上面的动作。这样，不停地把当前大顶堆的最大数调整到后面，一直到最后，整个数组就是有序的。

image

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
public class HeapSort {
    public static void main(String[] args) {
        int[] arr = {1,1,3,1,3,2,2,4,1,3};
        heapSort(arr);
        for (int anArr : arr) {
            System.out.print(anArr + " ");
        }
    }

    private static void heapSort(int[] arr){
        if(arr == null || arr.length < 2){
            return;
        }
        //第一次调整为大顶堆
        for(int i=0;i<arr.length;i++){
            heapInsert(arr,i);
        }
        int heapSize = arr.length;
        //第一个数与最后一个数交换，最后一个数就是最大的值，前面的数再调整为新的大顶堆
        //这样每次都将当前最大的数从数组的后面依次往前排，排到最后整个数组升序
        swap(arr,0,--heapSize);
        while(heapSize > 0){
            heapify(arr,0,heapSize);
            swap(arr,0,--heapSize);
        }
    }

    //如果当前的值是大于父节点的，就与父节点交换，使得大的数上浮
    private static void heapInsert(int[] arr, int index) {
        while(arr[index] > arr[(index-1)/2]){
            swap(arr,index,(index-1)/2);
            index = (index - 1)/2;
        }
    }

    //每次将最后一个数与第一个数交换后，我们要重新构建大顶堆，主要是将当前第一个数与自己的子节点进行比较，如果小于当前的子节点，则交换；否则不变，已经是大顶堆
    private static void heapify(int[] arr,int index,int heapSize){
        //拿到当前节点的左子节点
        int left = index * 2 + 1;
        //左子节点下标不能越界
        while(left < heapSize){
            //在右子节点也不越界的情况下，选出左右子节点中的较大者
            int largest = left+1 < heapSize && arr[left+1] > arr[left] ? left + 1 : left;
            //当前节点与左右子节点的最大者再比较
            largest = arr[largest] > arr[index] ? largest : index;
            //如果最大值就是当前节点，说明当前节点的值是大于左右两个子节点的，不需要交换，跳出循环
            if(largest == index){
                break;
            }
            //这个时候说明当前节点是小于某一个子节点的，那么就要进行交换，并且更新当前节点的坐标为子节点的而坐标，再更新左子节点，做下一次循环的比较
            swap(arr,largest,index);
            index = largest;
            left = index * 2 + 1;
        }
    }

    private static void swap(int[] arr, int i, int j) {
        int tmp = arr[i];
        arr[i] = arr[j];
        arr[j] = tmp;
    }
}

堆这个数据结构是非常重要的，因为他的动态调整的时间复杂度为logN，是非常低的。比如经典问题：快速在一串数字流中快速找到中位数等。