上一篇介绍了归并排序，本文介绍快速排序，顾名思义，应该是综合性能最好的排序了。在具体实现上，往上也有很多的版本，虽然大体思想一致，但是我觉得掌握其中一种最实用的方式就够了，本文的快排思想基于荷兰国旗问题演变，即所谓的三路快排，对于重复元素较多的场景是非常适合的，对于普通场景来说，性能也不弱。

1. 荷兰国旗问题

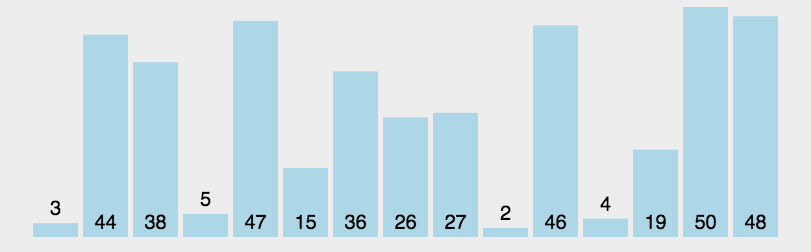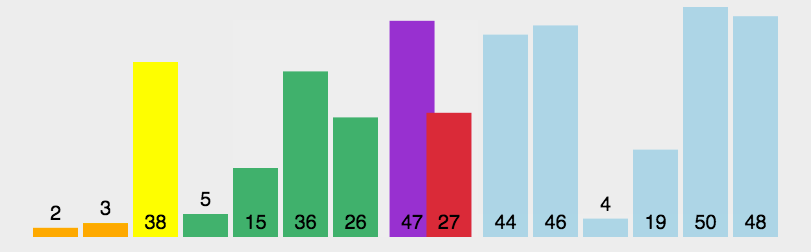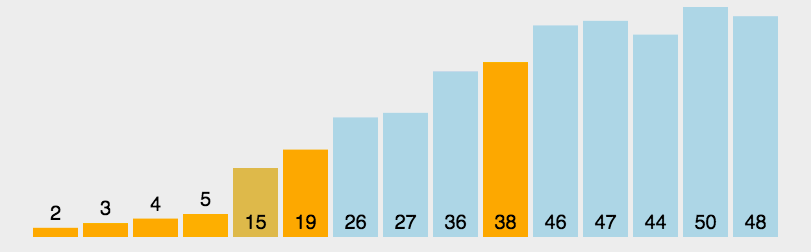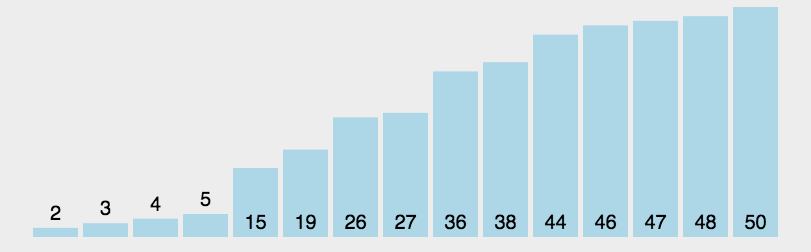
在研究快速排序之前，我们先来研究一下一个经典问题：荷兰国旗问题，我们的目标是给出一个num，将原来的数组中的值按照下面的规则进行排列：比num小的全放到num的左边，比bum大的全部放在右边，中间全是等于num的值。类似于荷兰国旗的三色旗。

imageimage

具体的算法思想看代码注释：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
/**
 * 荷兰国旗问题
 * 给定一个数组arr，和一个数num，请把小于num的数放在数组的左边，
 * 等于num的数放在数组的中间，大于num的数放在数组的右边。
 */
public class helan_flag_question_solve {

    public static void main(String[] args) {
        int[] arr = {1,1,3,1,3,2,2,1,1,3};
        solve(arr,0,arr.length-1,2);
        for(int i=0;i<arr.length;i++){
            System.out.print(arr[i] + " ");
        }
    }

    /**
     * 主要思想是：初始化的坐标分别为-1和N，就是取超出数组的范围，当前坐标是从0开始
     * 分为三种情况：如果当前等于num，那么指针后移一格即可
     * 如果当前小于num，那么就将当前和less+1交换位置，并且当前指针后移一格
     * 如果当前大于num，那么就将当前和more-1交换位置，当前位置不变继续判断、
     * 为什么与前面交换当前指针就要后移一格，但是与后面交换不用后移呢？
     * 我们知道，curr扫过的地方，curr当前指向的和前面的数肯定都是小于num的了，所以需要后移一个判断下一个元素
     * 但是从后面交换过来的，我们不知道这个交换过来的元素比num小还是大，所以对这个元素还需要判断一下
     */
    private static void solve(int[] arr,int L,int R,int num){
        int less = L-1;
        int more = R+1;
        int curr = L;
        while(curr < more){
            if(arr[curr] < num){
                swap(arr,++less,curr++);
            }else if(arr[curr] > num){
                swap(arr,--more,curr);
            }else{
                curr++;
            }
        }
    }

    private static void swap(int[] arr, int i, int j) {
        int tmp = arr[i];
        arr[i] = arr[j];
        arr[j] = tmp;
    }
}

这道题目一定一定要注意边界问题。下面的快排其实就是对荷兰国旗问题的递归操作。因此要想理解快排，需要先掌握荷兰国旗问题。

2. 快排

快速排序的基本思想：通过一趟排序将待排记录分隔成独立的两部分，其中一部分记录的关键字均比另一部分的关键字小，则可分别对这两部分记录继续进行排序，以达到整个序列有序。

快速排序使用分治法来把一个串（list）分为两个子串（sub-lists）。具体算法描述如下：

  • 从数列中挑出一个元素，称为 “基准”（pivot）；
  • 重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。在这个分区退出之后，该基准就处于数列的中间位置。这个称为分区（partition）操作；
  • 递归地（recursive）把小于基准值元素的子数列和大于基准值元素的子数列排序。

image

时间复杂度为O(N*logN),额外空间复杂度O(logN);

因为要记录划分区域的边界，所以需要一定的空间。这里划分的空间与二分的次数有关，所以需要O(logN)。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
private void quick_sort(int[] input,int low,int high){
    if(low < high){
        int[] p = partion(input,low,high);
        quick_sort(input,0,p[0]-1);
        quick_sort(input,p[1]+1,high);
    }
}

private int[] partion(int[] input,int L,int R){
    int less = L - 1;
    int more = R + 1;
    int curr = L;
    int num = input[L];
    while(curr < more){
        if(input[curr] < num){
            swap(input,++less,curr++);
        }else if(input[curr] > num){
            swap(input,curr,--more);
        }else{
            curr++;
        }
    }
    return new int[]{less,more};
}

private void swap(int[] arr, int i, int j) {
    int tmp = arr[i];
    arr[i] = arr[j];
    arr[j] = tmp;
}

快排存在的一个问题是：可能划分出来两边数组很偏，排序效率就会变差。可以用随机快排进行改进。

思路：随机选一个数与数组最后一个数交换。

1
swap(arr,L+(int)(Math.random()*(R-L+1)),R);

相比于经典快排，这个优化的快排的优点在于：每一次partition之后，就可能会揪出一串的相等数字，然后左边全是小于这个数，右边都是大于这个数。而经典快排每次只找出一个数字来，左边是小于等于这个数，右边是大于这个数。很显然，优化后的快排要快一点。

这种从荷兰国旗演变过来的快排，对于重复元素较多的时候是非常有利的，因此这种是我比较喜欢的一种写法，这也意味着快排的实现上有一些差异，但是主要的思想是一致的，即分治处理。