在之前我们介绍的都是比较排序算法，在结果中各元素的次序都基于输入元素间的比较。而任何比较排序算法在最坏情况下都要用 O(NlgN) 此比较来排序。而非基于比较的排序，如计数排序，桶排序，和在此基础上的基数排序，则可以突破O(NlogN)时间下限。但要注意的是，非基于比较的排序算法的使用都是有条件限制的，例如元素的大小限制，相反，基于比较的排序则没有这种限制(在一定范围内)。但并非因为有条件限制就会使非基于比较的排序算法变得无用，对于特定场合有着特殊的性质数据，非基于比较的排序算法则能够非常巧妙地解决。

计数排序

计数排序不是基于比较的排序算法，其核心在于将输入的数据值转化为键存储在额外开辟的数组空间中。 作为一种线性时间复杂度的排序，计数排序要求输入的数据必须是有确定范围的整数。

  • 找出待排序的数组中最大和最小的元素；
  • 统计数组中每个值为i的元素出现的次数，存入数组C的第i项；
  • 对所有的计数累加（从C中的第一个元素开始，每一项和前一项相加）；
  • 反向填充目标数组：将每个元素i放在新数组的第C(i)项，每放一个元素就将C(i)减去1。

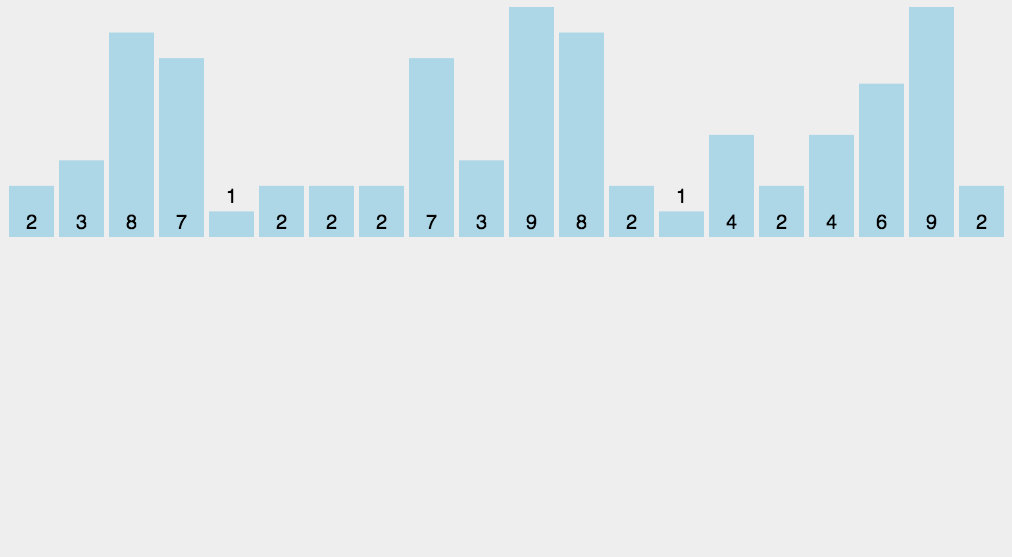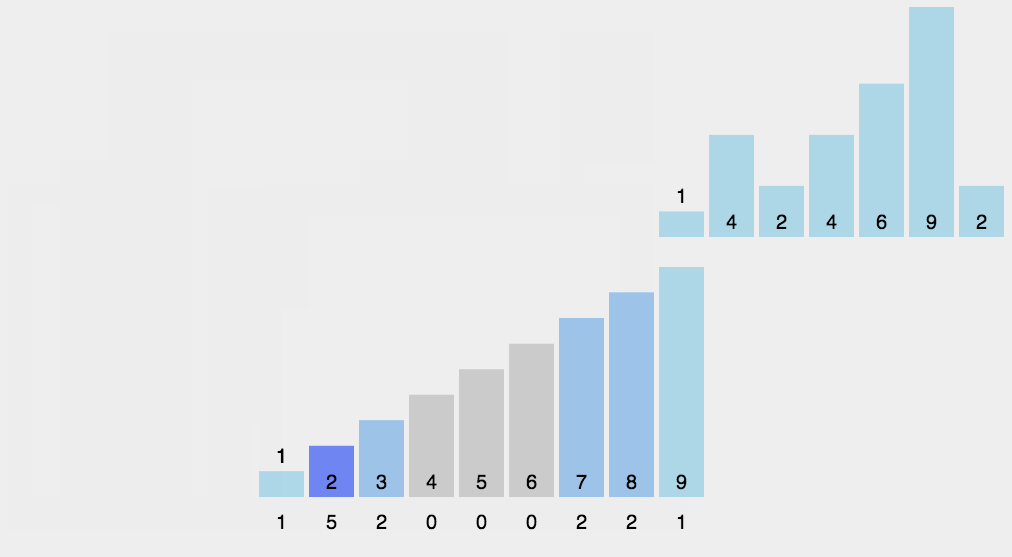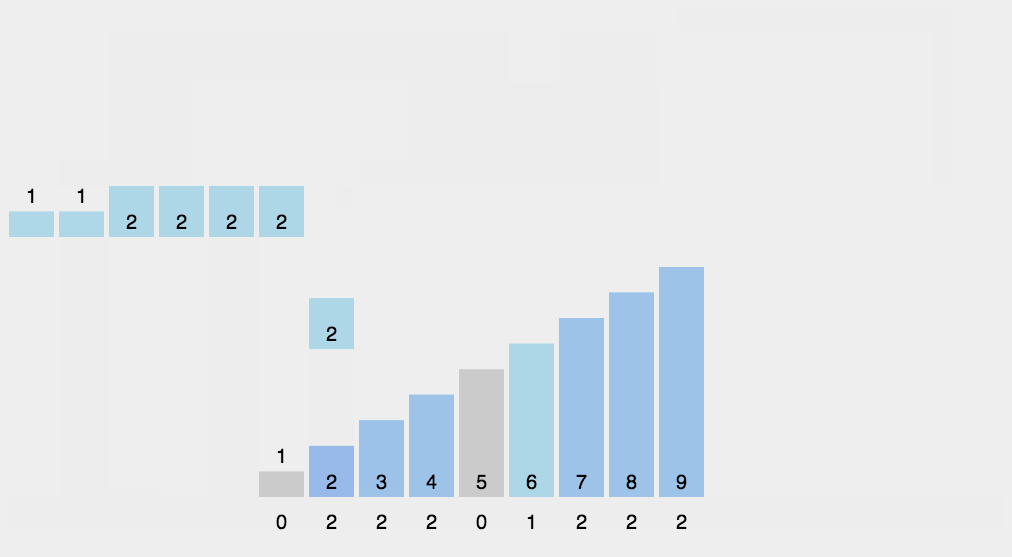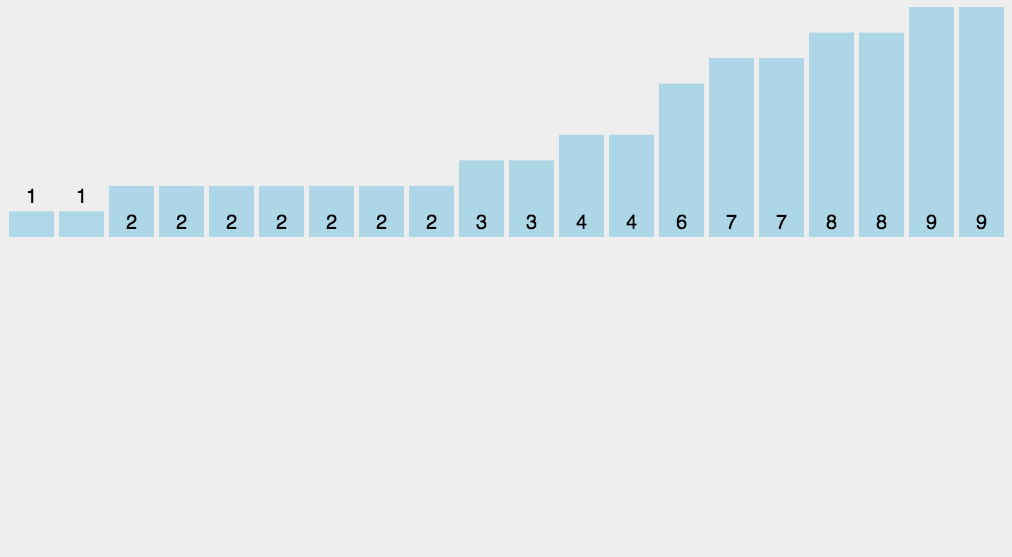
image

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
//maxVal为传入的数组的最大值
private int[] countSort(int[] array,int maxVal){
    // 1.根据最大值可以确定辅助数组的长度
    int[] helper = new int[maxVal+1];
    //2.遍历array数组，统计每个元素出现的次数，记录在辅助数组对应索引处
    for(int i=0;i<array.length;i++){
        helper[array[i]]++;
    }
    //3.遍历辅助数组，覆盖原数组
    int index = 0;
    for(int i=0;i<maxVal+1;i++){
        while (helper[i] > 0){
            array[index++] = i;
            helper[i]--;
        }
    }
    return array;
}

桶排序

桶排序是计数排序的升级版。它利用了函数的映射关系，高效与否的关键就在于这个映射函数的确定。桶排序 (Bucket sort)的工作的原理：假设输入数据服从均匀分布，将数据分到有限数量的桶里，每个桶再分别排序.

  • 找出待排序数组中的最大值max、最小值min
  • 我们使用动态数组 ArrayList 作为桶，桶里放的元素也用 ArrayList 存储。桶的数量为(max-min)/arr.length+1
  • 遍历数组 arr，计算每个元素 arr[i] 放的桶
  • 每个桶各自排序
  • 遍历桶数组，把排序好的元素放进输出数组

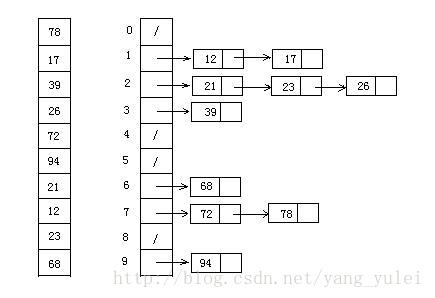
image

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
private static int[] bucketSort(int[] arr){
    //1.确定出数组的最大值和最小值
    int max = Integer.MIN_VALUE;
    int min = Integer.MAX_VALUE;
    for(int i=0;i<arr.length;i++){
        max = Math.max(arr[i],max);
        min = Math.min(arr[i],min);
    }
    
    //2.根据最大值和最小值确定桶的数量，并且初始化每个桶
    int buctetSize = (max-min)%arr.length + 1;
    ArrayList<ArrayList<Integer>> bucket = new ArrayList<>(buctetSize);
    for(int i=0;i<buctetSize;i++){
        bucket.add(new ArrayList<>());
    }
    
    //3.类似于hashmap，将其元素放到对应下标的桶中
    for(int i=0;i<arr.length;i++){
        int num = (arr[i] - min)%buctetSize;
        bucket.get(num).add(arr[i]);
    }

    //4.对每个桶中的元素都要进行排序
    for(int i=0;i<buctetSize;i++){
        Collections.sort(bucket.get(i));
    }
    
    System.out.println(bucket.toString());
    
    //5.遍历所有的桶，类似于计数排序一样覆盖原数组得到有序的序列
    int arrIndex = 0;
    for(int i=0;i<buctetSize;i++){
        int index = 0;
        int sum = bucket.get(i).size();
        while(sum > 0){
            arr[arrIndex++] = bucket.get(i).get(index++);
            sum--;
        }
    }

    return arr;
}

基数排序

基数排序(Radix Sort)是桶排序的扩展，它的基本思想是：将整数按位数切割成不同的数字，然后按每个位数分别比较。

通过基数排序对数组{53, 3, 542, 748, 14, 214, 154, 63, 616}，它的示意图如下：

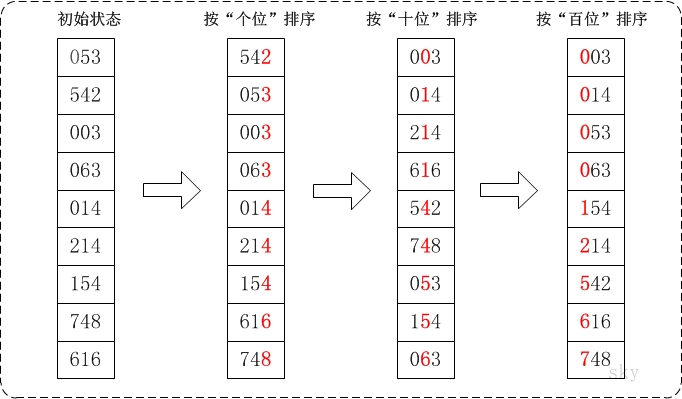
image

在上图中，首先将所有待比较数值统一为统一位数长度，接着从最低位开始，依次进行排序。

  • 按照个位数进行排序。
  • 按照十位数进行排序。
  • 按照百位数进行排序。
    排序后，数列就变成了一个有序序列。

在理解了基本的思想之后，下面以一个简单的例子辅助理解程序思想。

首先我们有以下这个数组：

1
int[] arrays = {6,  4322, 432, 344, 55 };

现在我们有10个桶子，每个桶子下能装载arrays.length个数字

1
int[][] buckets = new int[arrays.length][10];

效果如下：

image

第一趟分配与回收:将数组的每个个位数进行分配到不同的桶子上

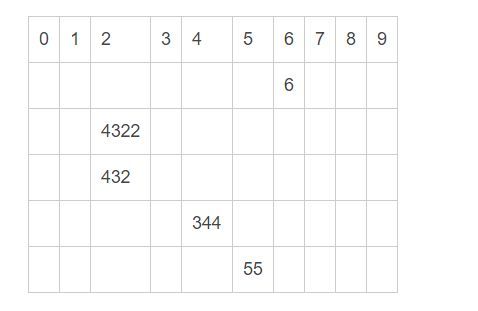
image

分配完之后，我们按照顺序来进行回收：得到的结果应该是这样子的：{4322,432,344,55,6}

第二趟分配与回收:将数组的每个十位数进行分配到不同的桶子上(像6这样的数，往前边补0)

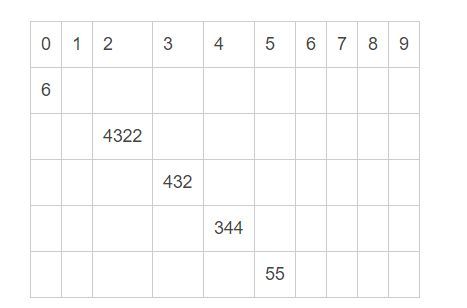
image

分配完之后，我们按照顺序来进行回收：得到的结果应该是这样子的：{6,4322,432,344,55}

第三趟分配与回收:将数组的每个百位数进行分配到不同的桶子上(像6、55这样的数，往前边补0)

image

分配完之后，我们按照顺序来进行回收：得到的结果应该是这样子的：{6,55,4322,344,432}

第四趟分配与回收:将数组的每个百位数进行分配到不同的桶子上(像6、55，344，432这样的数，往前边补0)

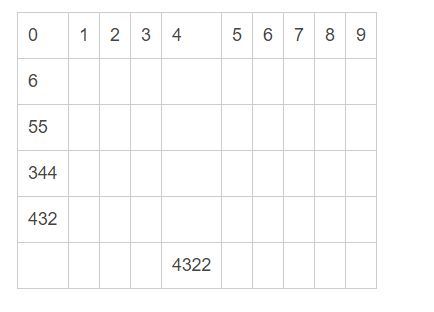
image

分配完之后，我们按照顺序来进行回收：得到的结果应该是这样子的：{6,55,344,432,4322}

理解了上面，代码也就非常容易理解了：

获取这个数组的最大值，这里用递归来实现一下：

1
2
3
4
5
6
7
8
private static int getMax(int[] arr,int L,int R){
    if(L == R){
        return arr[L];
    }
    int a = arr[L];
    int b = getMax(arr,L+1,R);
    return a > b ? a : b;
}

基数排序：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
public static int[] radixSort(int[] arr) {
    //求得数组最大值
    int max = getMax(arr,0,arr.length-1);
    
    //最大数的位数就是我们要分配的次数
    for(int i = 1 ; max / i > 0 ; i *= 10){
    
        //构造arr.length行，10列的二维数组
        int[][] buckets = new int[arr.length][10];
        
        //求数组每个位，如个位，十位等，根据该位的数字放到对应的二维数组里
        for(int j=0;j<arr.length;j++){
            int num = (arr[j]/i)%10;
            buckets[j][num] = arr[j];
        }
        
        //一次放完之后，就要回收起来放进原来的数组中，等待下一次的重新分配
        int index = 0;
        for(int k=0;k<10;k++){
            for(int j=0;j<arr.length;j++){
                if(buckets[j][k] != 0){
                    arr[index++] = buckets[j][k];
                }
            }
        }
    }
    return arr;
}

基数排序要理解起来并不困难，不过值得注意的是：基数排序对有负数和0的数列难以进行排序

  • 因此，往往有0和负数的数组一般我们都不用基数来进行排序

基数排序的要点就两个：

  • 分配：按照元素的大小来放入不同的桶子里
  • 回收：将桶子里的元素按桶子顺序重新放到数组中
  • 重复…两个步骤