基础算法13-动态规划入门
在求解某个序列的最优解的时候,经常会用到动态规划来解决。动态规划的核心是找出一个关系式,并且借助于选或者不选找出两个迭代的路径进行比较,最终遍历整个序列之后也就得到了选或者不选中的最优解,也就是整个序列的最优解。由于还是比较复杂的,所以是对动态规划学习的一个入门之作。
什么是动态规划
动态规划算法通常用于求解具有某种最优性质的问题。在这类问题中,可能会有许多可行解。每一个解都对应于一个值,我们希望找到具有最优值的解。动态规划算法与分治法类似,其基本思想也是将待求解问题分解成若干个子问题,先求解子问题,然后从这些子问题的解得到原问题的解。与分治法不同的是,适合于用动态规划求解的问题,经分解得到子问题往往不是互相独立的。若用分治法来解这类问题,则分解得到的子问题数目太多,有些子问题被重复计算了很多次。如果我们能够保存已解决的子问题的答案,而在需要时再找出已求得的答案,这样就可以避免大量的重复计算,节省时间。我们可以用一个表来记录所有已解的子问题的答案。不管该子问题以后是否被用到,只要它被计算过,就将其结果填入表中。这就是动态规划法的基本思路。引自百度百科
我们以解决一个小例子入手。
例子
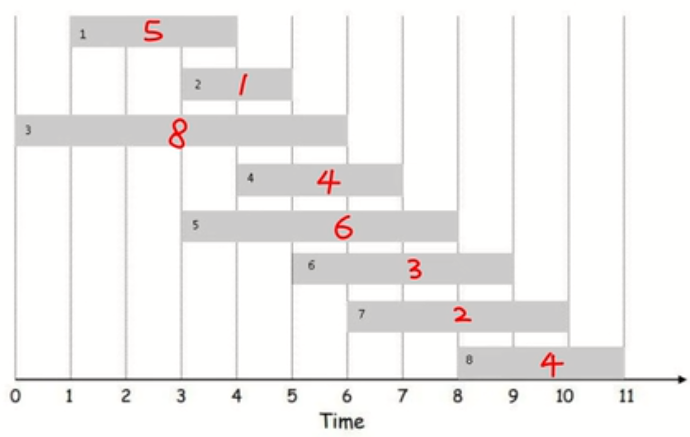
如图所示,横轴是时间,上面是一段一段的长方形,将其想象为工作时间,比如第一块,是1点到4点的工作,收益为5,第二块是3点到5点的工作,收益是1.一个人不可能同时做两份工作,即时间不能重叠,请问这个人如何安排做哪几个工作最终收益是最大的?
这道题目如何思考呢?正常的思维可能是:假设我做第一个工作,那么我做完之后只能做第四个工作才不冲突,做完第四个再做第8个工作,但是这个不一定是最优解,那么我还需要判断各种情况,比如我第一个工作做完了可能会去做第6个工作,好像很混乱,无从下手了。
各位,现在转换一下思维,我们不从第一个开始考虑,我们从最后一个开始考虑。怎么考虑呢?
对于第八份工作而言,我有两个选择,一个是做,一个是不做。不做就很简单,我再从第七份工作开始考虑。做的话,那么我下面就要考虑前面可以做的最好的工作了,我们发现第五份工作以及之前的工作都可以做做,那么就是说对前五个工作找到一个收益最大的方案就即刻。我们用OPT(i)函数表示第i个参数之前最优解的话,那么对于上述可以表示为:
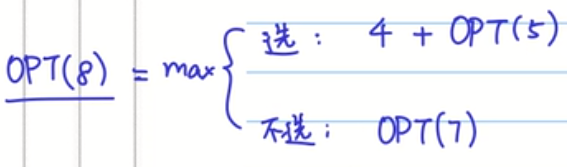
其实根据这个情况,我们递推出一个通用一点的关系式:

对于这个prev(i)表示在选择当前i元素之后,可以考虑的最优的子集的第一个元素(这个元素是反着找的)。比如选了8,那么我前面能考虑的只能是1,2,3,4,5这几块,因为6和7都不能选的。即使3或者4可能不满足条件,但是我们只要找到最接近的5即可。
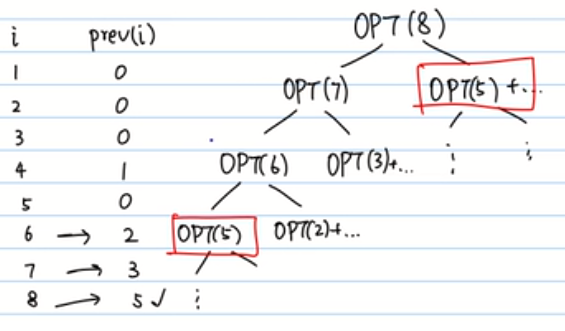
我们会发现这种问题是存在重叠子问题的,这个就是问题的关键,一个问题分解为若干子问题,为了避免重复的计算,是需要将这些子问题存储起来的,下次用到的时候直接去内存中查出来即可。
这个问题根据上面的表达式就可以求出最优的一个情况。对于这个例子我们只需要理解它的解体思想即可,下面我们真正实践一个题目。
小偷偷东西
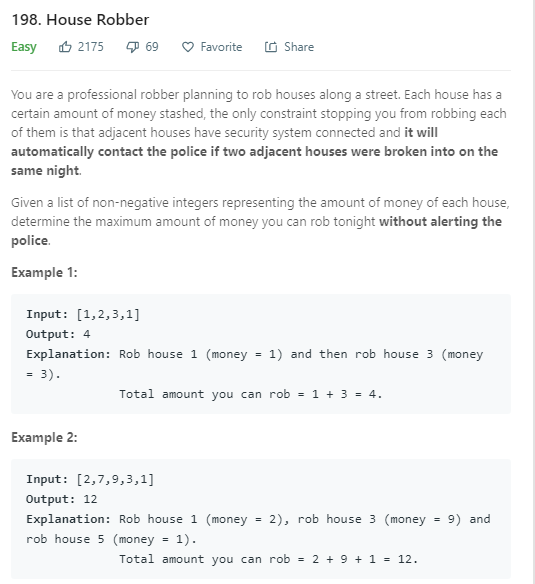
这个问题大概就是说,一个小偷偷东西,但是它不能偷相邻的两家人的东西,这样会被抓住,只能隔着偷,请问,怎么偷才能利益最大化,因为每个房子的价值不一样,假如有两家,一家有100块,一家有一个亿,你选择不好,选了100的那家,那就亏大发了,一个亿的下次再来偷吧。
按照上面的思路,我们来思考这个问题,我们从最后一家开始考虑,选择就两个,偷或者不偷,偷了会怎么样,不偷会怎么样,其实关系式跟上面是差不多的,我偷了的话,比如偷的是n,那么下次只能从n-2开始考虑它的最大价值方案。不偷的话,就是考虑n-1的最大价值方案。
最简单的实现就是递归来实现,主要是要考虑一下函数的出口条件,即偷到第一家了是什么样,以及第一家之前没有人家了怎么办。代码如下:
1 | class Solution { |
很可惜,虽然逻辑上正确,但是由于是递归,在数据规模大一点之后,就不行了,因为我们前面也说到,存在大量的重叠子问题,问题多一个输入,那么计算的规模就要乘上2,所以时间复杂度为2^n这个级别。所以此方案放在leetcode上会超时,下面就是想办法把他改成非递归的版本。
前面提到,计算出来的子问题完全可以存在一个地方,下次要用直接取。OK,用非递归版本的数组版本实现是:
1 | class Solution { |
主体还是上面提到的那个关系,只是我们将子问题的结果放在了一个临时数组中。临时数组中存放的都是子问题的最优解。比如tmp[1]里面存放的就是前两个元素中最大值,即最优解。当计算前三个数中最优解的时候,我只要做一个选择,即要不要选择nums[2]这个元素,选择的话,那么我就从tmp[2-2]中得到最优解,加起来就是当前最优解,不选择的话,就从tmp[2-1]中选择最优解。依次下去,tmp中最后一个值就是整个序列中组合的最优解了。
这里注意一下,这里其实是记忆化搜索的思想来实现的,我们可以注意到,其实是自顶向下来看的,从第一个数字来一直推到最后。然而动态规划的思想是从底向上的,参见第一个递归版本的实现。我们先考虑的是最终的n,而不是考虑从0开始。所以在设计思想上是有所区别的,但是又是非常类似,有的人将他们归位一类,我想,它们在大多数场景下可以互换的化,可以认为都是广义上的DP算法吧,因为DP毕竟只是一种思想,正过来实现反过来实现也未尝不可。
我们用一个数组来存放子问题的最优解,大大降低了时间复杂度,leetcode上也顺利通过。其实这个是一种记忆化搜索的思想,上面这个用了一个数组,其实完全没有必要用数组,用两个变量即可:
1 | class Solution { |
时间复杂度不变,空间上占用的更少了。下面我们还是从底向上的思想来解决一下这个问题吧。所以我们还是从最后一个元素开始思考,从后往前找,一直找到第一个结束。
1 | class Solution { |
运行下来的效果是要比上面的记忆化搜索效果差的,但是都通过了。
⭐墙裂推荐:
部分图片截取于他的视频。