剑指offer第三十题。

题目描述

HZ偶尔会拿些专业问题来忽悠那些非计算机专业的同学。今天测试组开完会后,他又发话了:在古老的一维模式识别中,常常需要计算连续子向量的最大和,当向量全为正数的时候,问题很好解决。但是,如果向量中包含负数,是否应该包含某个负数,并期望旁边的正数会弥补它呢？例如:{6,-3,-2,7,-15,1,2,2},连续子向量的最大和为8(从第0个开始,到第3个为止)。给一个数组，返回它的最大连续子序列的和，你会不会被他忽悠住？(子向量的长度至少是1)

解题思路

这一题，我们可以用动态规划的思想来解决。我们不断往前试，试到最后。这里从前往后或者从后往前开始算都是一样的。我这里就从后往前开始算吧。

主要的一个公式是 max = Max(array[i] , array[i]+max)

基本思想就是：max代表后面已经扫描过的数组中的最优解，即最大连续字串的和。

此时max加上自己的值与自己比较，如果还不如自己，那么显然扫描过的数组可以抛弃。直接从自己开始再算即可。如果比自己大，那么就可以把自己也包含进这个数组中。

所以，核心思想是：看已经算过的数组的价值有没有给当前元素拖后腿，如果拖后腿就砍掉。

如图所示：

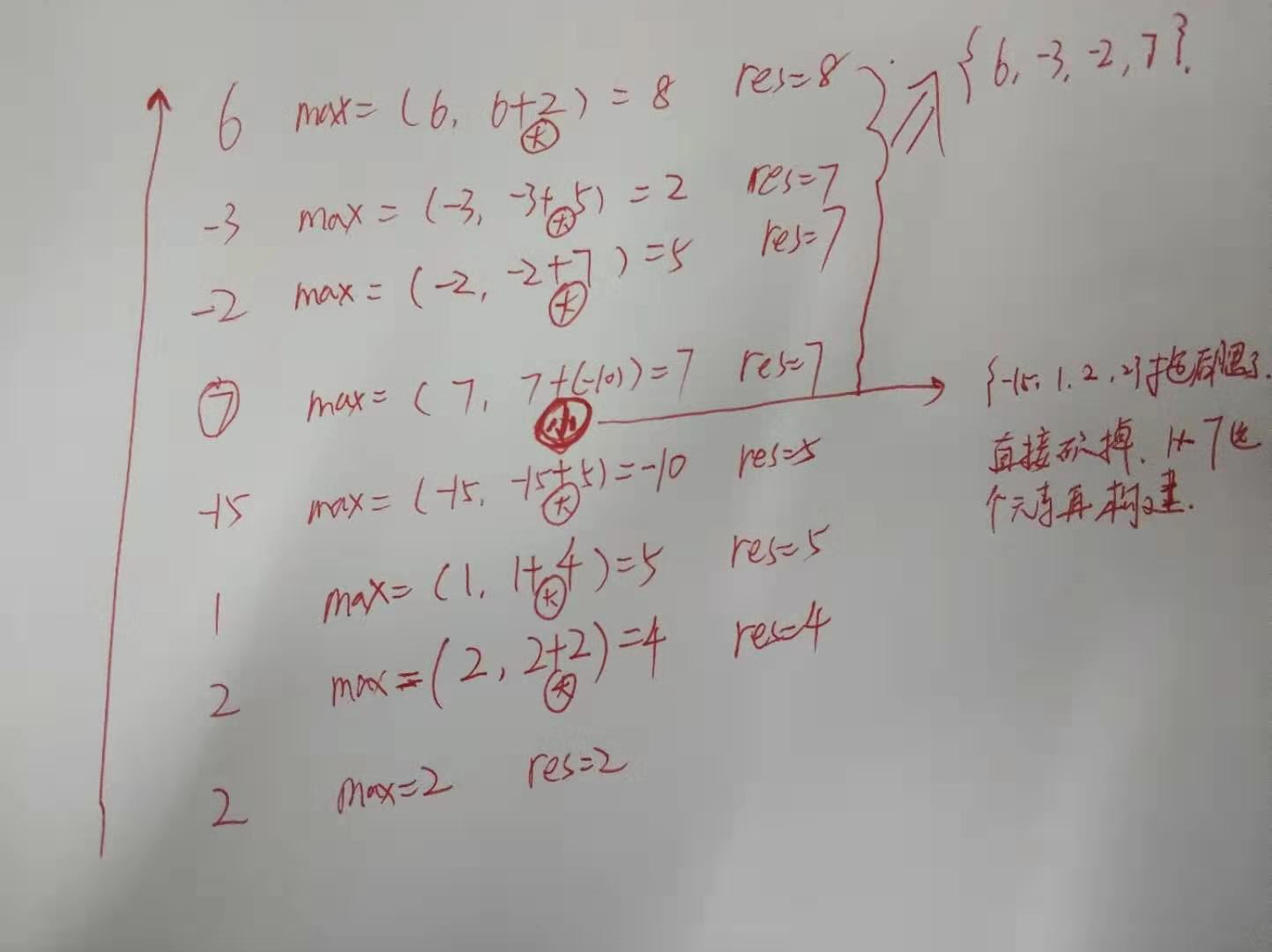
image

我的答案

容我插一嘴，自底向上考虑问题比较符合动态规划的思想，但是这里好像没什么区别。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
public class Solution {
    public int FindGreatestSumOfSubArray(int[] array) {
        if(array.length == 0 || array == null){
            return 0;
        }
        
        int index = array.length-1;
        
        int max = array[index];
        int res = array[index];
        
        for(int i=index-1;i>=0;i--){
            max = Math.max(array[i],array[i]+max);
            res = Math.max(res,max);
        }
        
        return res;
    }
}